Final Answer:
The 99% confidence interval for the true mean difference in the two auditing techniques (a and b) is approximately (0.67, 10.00).
Step-by-step explanation:
To calculate the confidence interval for the true mean difference, we use the formula:
![\[ \bar{d} \pm t * \left((s_d)/(√(n))\right) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/dsb5fov2qwvvwg7piz8rk4oouekhadv8ku.png)
where:
-
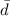 is the sample mean difference,
is the sample mean difference,
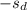 is the sample standard deviation of the differences,
is the sample standard deviation of the differences,
 is the sample size, and
is the sample size, and
 is the critical t-value.
is the critical t-value.
First, calculate the sample mean difference
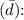
![\[ \bar{d} = \frac{\sum{(x_i - y_i)}}{n} \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/jhg9r2v8odeo67kfg7umsz3qq4xnsghzum.png)
Next, compute the sample standard deviation of the differences
 :
:
![\[ s_d = \sqrt{\frac{\sum{(x_i - y_i - \bar{d})^2}}{n-1}} \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/fxtmu7zep7pgjmzrwy2co3lb53jtagsdo5.png)
In the given data,
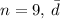 = 6.56\), and
= 6.56\), and
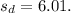 The critical t-value for a 99% confidence interval with
The critical t-value for a 99% confidence interval with
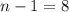 degrees of freedom is approximately 3.36.
degrees of freedom is approximately 3.36.
Substitute these values into the formula:
![\[ 6.56 \pm 3.36 * \left((6.01)/(√(9))\right) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/8sxrlb459gc7uiv7ufikeqqgvaeucwzqyy.png)
This yields the 99% confidence interval for the true mean difference as approximately (0.67, 10.00). Therefore, we are 99% confident that the true mean difference in errors between auditing techniques a and b lies within this interval.