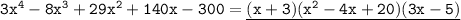Answer:
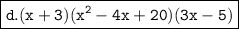
Given:
The polynomial is
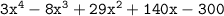
The roots are -3 and 2 + 4i.
Solution:
Let's factorize the given polynomial
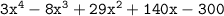 , we can use the roots provided in the question:
, we can use the roots provided in the question:
The roots are x = -3, x = 2 + 4i, and x = 2 - 4i.
When a polynomial has a root, its corresponding factor is (x - root). So, for the given roots, the corresponding factors are:
1. For x = -3, the corresponding factor is (x + 3).
2. For x = 2 + 4i, the corresponding factor is (x - (2 + 4i)) = (x - 2 - 4i).
3. For x = 2 - 4i, the corresponding factor is (x - (2 - 4i)) = (x - 2 + 4i).
Now, we can find the factorization:
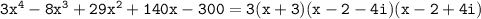
As mentioned earlier, the factor (x - 2 - 4i)(x - 2 + 4i) can be simplified using the difference of squares formula:
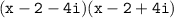
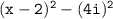
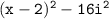
![\tt (x - 2)^2 - 16(-1) [since\:\: i^2 = -1]](https://img.qammunity.org/2024/formulas/mathematics/college/ro1y5jl92d6nkyyhrxzsuyjhhiwytjgjmm.png)
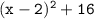
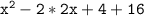
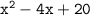
So, the final factorization is:

By multiplying, we get
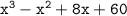
Find a factorization of
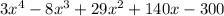 , given that -3 and 2 + 4i are roots.
, given that -3 and 2 + 4i are roots.
since it is a cubic equation but the given expression is in a quadratic equation.
We can find the remaining factor doing long division.
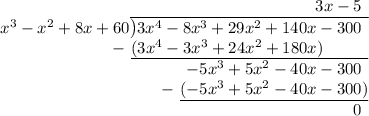
Therefore, the factors are: