Final Answer:
Each semiannual payment is approximately $1,838.53.
Step-by-step explanation:
To calculate the semiannual payment for the amortization of the debt, we can use the formula for the present value of an annuity:
![\[ PVA = P * \left(1 - (1)/((1 + r)^(nt))\right) / r \]](https://img.qammunity.org/2024/formulas/business/high-school/bzfil43ovim8h9gysy3cgh4baek4my0f7d.png)
Where:
- \( P \) is the periodic payment,
- \( r \) is the interest rate per period,
- \( n \) is the total number of periods (in this case, semiannual payments),
- \( t \) is the total number of years.
In this scenario:
-
 is the present value of the debt, which is $9,000,
is the present value of the debt, which is $9,000,
-
 is the interest rate per period (13% compounded semiannually, so \
is the interest rate per period (13% compounded semiannually, so \
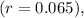
-
 ) is the total number of semiannual periods (8 payments in total, so
) is the total number of semiannual periods (8 payments in total, so
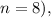
-
 is the total number of years (1 year for 8 semiannual periods, so
is the total number of years (1 year for 8 semiannual periods, so
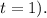
Substitute these values into the formula and solve for \( P \) to find the semiannual payment.
![\[ 9000 = P * \left(1 - (1)/((1 + 0.065)^(8))\right) / 0.065 \]](https://img.qammunity.org/2024/formulas/business/high-school/w9ntp7jt5xsap34fvlh497l1e5gaxzrf95.png)
![\[ P \approx (9000)/(\left(1 - (1)/((1 + 0.065)^(8))\right) / 0.065) \]](https://img.qammunity.org/2024/formulas/business/high-school/3ebkcr6xig8izxirdu9bchqve02atg0twx.png)
![\[ P \approx 1838.53 \]](https://img.qammunity.org/2024/formulas/business/high-school/e41ztmvjwrafuc6kyhs8b07gwljwzmoymj.png)
Therefore, each semiannual payment is approximately $1,838.53.