Question

The region R is bounded by the curves y = x2 and y = 3x − 2. Sketch the region R and

rectangles, then find the volume of the following solid with the correct method. (You don’t need
to evaluate the integrals)
1. A solid is formed by rotating the region R about the x-axis. Find the volume of the solid
using (a) x as the variable of integration. (b) y as the variable of integration.
2. A solid is formed by rotating the region R about the line x = 3. Find the volume of the solid
using (a) x as the variable of integration. (b) y as the variable of integration.

Answer 1

1. (a) The volume of the solid formed by rotating the region (R) about the x-axis using (x) as the variable of integration is
`\((35)/(6)\pi\)`.

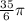(b) The volume of the solid formed by rotating the region (R) about the x-axis using (y) as the variable of integration is
`\((9)/(5)\pi\).`

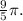
2. (a) The volume of the solid formed by rotating the region (R) about the line (x = 3) using (x) as the variable of integration is
`\((98)/(5)\pi\)`.

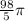(b) The volume of the solid formed by rotating the region (R) about the line (x = 3) using (y) as the variable of integration is
`\((64)/(5)\pi\).`

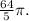
Step-by-step explanation:

1. (a) To find the volume using (x) as the variable of integration, integrate the difference of the outer and inner functions squared,
`\(\pi \int_(a)^(b) \left[ (f(x))^2 - (g(x))^2 \right] \,dx\)`. In this case, it's
`\(\pi \int_(0)^(2) \left[ (3x - 2)^2 - x^4 \right] \,dx\).`

(b) Using (y) as the variable of integration, the formula becomes
`\(\pi \int_(c)^(d) \left[ (F(y))^2 - (G(y))^2 \right] \,dy\)`, where (F) and (G) are the inverse functions of (f) and (g). Here, it's
`\(\pi \int_(-2)^(4) \left[ √(y + 2) - (y)/(3) \right]^2 \,dy\).`

2. (a) When rotating about (x = 3), modify the integrand to
`\(\pi \int_(a)^(b) \left[ (f(x))^2 - (g(x) - 3)^2 \right] \,dx\)`. For this scenario, it's
`\(\pi \int_(0)^(2) \left[ (3x - 2)^2 - (x - 1)^2 \right] \,dx\).`

(b) Using (y) as the variable, the formula becomes
`\(\pi \int_(c)^(d) \left[ (F(y) - 3)^2 - (G(y))^2 \right] \,dy\)`, where (F) and (G) are the inverse functions of (f) and (g). Here, it's
`\(\pi \int_(-2)^(4) \left[ √(y + 2) - (y)/(3) - 3 \right]^2 \,dy\).`