Question

a river has a current of 2 miles per hour. Billy travels in a canoe 22 miles downstream in the same time it takes to go 16 miles upstream. Find the speed of the boat in still water

Answer 1

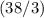`(38/3)` miles per hour.

Step-by-step explanation:

To solve this question, let the speed of the boat in still water be the unknown variable. Express the time required to travel
`22` miles upstream and
`16` miles downstream in terms of this speed. Using the fact that the time required to finish these trips should be equal, set up and solve an equation to obtain the value of this speed.

Let
`v` miles per hour be the speed of this boat is still water.

When the boat is travelling downstream in the direction of the current, ground speed of the boat would be
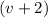`(v + 2)` miles per hour. The time required to travel the required
`22` miles downstream at this ground speed would be
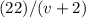`(22) / (v + 2)` hours.

When the boat is travelling upstream against the current, ground speed of the boat would be
`(v - 2)` miles per hour. The time required to travel
`16` miles upstream at this ground speed would be
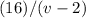`(16) / (v - 2)` hours.

It is given that the time required to finish these two trips should be equal. In other words:

`\displaystyle (22)/(v + 2) = (16)/(v - 2)`.

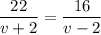Rearrange this equation and solve for
`v`, the speed of this boat in still water:

`16\, (v + 2) = 22\, (v - 2)`.

`\displaystyle v = (38)/(3)`.

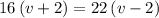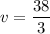In other words, the speed of this boat should be
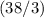`(38 / 3)` miles per hour while in still water.