The maximal volume of the box with a square base and surface area 44 is
 cubic units.
cubic units.
Let's denote the side length of the square base as
 and the height of the box as
and the height of the box as
 . Given that the surface area of the box is 44, we can set up an equation using the formula for the surface area of a box:
. Given that the surface area of the box is 44, we can set up an equation using the formula for the surface area of a box:

For a square base, the base area is
 and the perimeter is
and the perimeter is
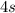 . The surface area given is 44, so:
. The surface area given is 44, so:
![\[2s^2 + 4sh = 44\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/jfrzd5yfij0spt7xcz3m9enbcl46wfgou5.png)
Now, we want to express the volume of the box in terms of
 and
and
 . The volume of a box is given by the formula:
. The volume of a box is given by the formula:
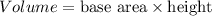
For a square base, the base area is
 , so the volume is
, so the volume is
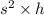 .
.
The goal is to find the dimensions that maximize the volume. We can use the fact that the side length of the base is given as
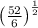 to determine the dimensions that result in the maximal volume.
to determine the dimensions that result in the maximal volume.
Let's solve for
 and
and
 using the surface area equation and then find the maximum volume:
using the surface area equation and then find the maximum volume:
Given:
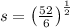
![\[2s^2 + 4sh = 44\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/jfrzd5yfij0spt7xcz3m9enbcl46wfgou5.png)
![\[2 * \left((52)/(6)\right) + 4 * \left((52)/(6)\right)^{(1)/(2)} * h = 44\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/4ywdpslbjmac22tkqwx0hz21smp8qkdqi7.png)
![\[(104)/(6) + 4 * \left((52)/(6)\right)^{(1)/(2)} * h = 44\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/fj0c3ycxai6emady03ev3qi4g2ul1il0mo.png)
![\[4 * \left((52)/(6)\right)^{(1)/(2)} * h = 44 - (104)/(6)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/h53po6rfpy2t06q1lbisqpwwcy6hpuy1rl.png)
![\[4 * \left((52)/(6)\right)^{(1)/(2)} * h = (176)/(6)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/b4k8num7pby2org5tje3onz9xe41731elp.png)
![\[h = \frac{(176)/(6)}{4 * \left((52)/(6)\right)^{(1)/(2)}}\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/eyoaz8snuqp82bjcwt51no2nv9amugo9z9.png)
![\[h = \frac{44}{\left((52)/(6)\right)^{(1)/(2)}}\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/c5zx28boqmz67pwheic9q54jixitaghsyi.png)
So, the height of the box is
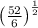 .
.
Now, let's calculate the volume:
![\[V = s^2 * h\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/bcmnhzvlbafip5l78gairzgtcbyqrytgdn.png)
![\[V = \left((52)/(6)\right)^{(1)/(2)} * \left((52)/(6)\right)^{(1)/(2)}\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/kxb5cpyvdrtfvz12semrgngx8eci5nih02.png)
![\[V = (52)/(6)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/bjbdrnooyaptccpsa8m5d121ip6f26ipm6.png)
Therefore, The answer is
 cubic units.
cubic units.
The complete question is here:
Find the dimensions of a box with a square base with surface area 44 and the maximal volume.
(Use symbolic notation and fractions where needed.)