Question

Volume of a sphere = 7³, where r is the radius.

The shape below is made from a cylinder and a hemisphere.
The volume of this shape is
2684 cm³.
π
3
Work out the height of the cylinder.
Give your answer to 1 d. p.
8 cm

Answer 1

8.6 cm (1 d.p.)

Explanation:

The given three-dimensional object is made from a cylinder and a hemisphere. The radius of the object is 8 cm, and its volume is 2684π/3 cm³.

The equation for the volume of a cylinder is πr²h, where r is the radius and h is the height.

The equation for the volume of a hemisphere is half the volume of a sphere. Therefore, the volume of a hemisphere is 2πr³/3, where r is the radius.

To determine the height of the cylinder (h), set the sum of the two volume equations to the given volume, substitute r = 8, and solve for h:

`\begin{aligned}\sf V_(cylinder)+V_(hemisphere)&=\sf V_(total)\\\\\pi r^2h + (2\pi r^3)/(3) &=(2684 \pi)/(3)\\\\\pi \cdot 8^2 \cdot h + (2\pi \cdot 8^3)/(3) &=(2684 \pi)/(3)\\\\64\pi h + (1024\pi)/(3) &=(2684 \pi)/(3)\\\\64h + (1024)/(3) &=(2684)/(3)\\\\64h&=(1660)/(3)\\\\h&=(415)/(48)\\\\h&=8.6458333...\\\\h&=8.6\; \sf cm\end{aligned}`

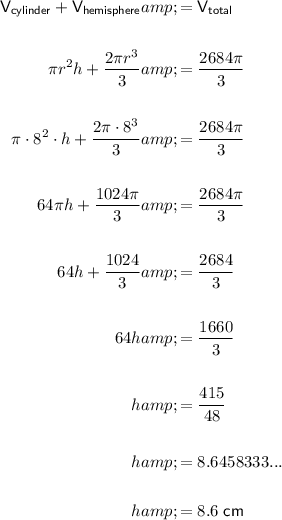
Therefore, the height of the cylinder is 8.6 cm (1 d.p.).