Question

Jennifer is your first individual client. She is a college student at age 20. She asks you to help her set up a financial plan to make sure that she can have adequate savings at her age 65 when she plans to retire. If she thinks she needs to have $1.25 million when she retires, with an average annual interest rate 8%, which was calculated based on some historical data, how much money does she need to save every month from now to her age 65 ?

Previous question

Answer 1

To calculate how much Jennifer needs to save every month from now until age 65, we can use the formula for compound interest. Plugging in the given values and solving for monthly savings will give us the amount Jennifer needs to save.

Step-by-step explanation:

To calculate how much Jennifer needs to save every month from now until age 65, we can use the formula for compound interest:

Amount = Monthly Savings x ((1 + Interest Rate/12)^(Number of Years x 12) - 1) / (Interest Rate/12)

Plugging in the given values:

Amount = Monthly Savings x ((1 + 0.08/12)^(45 * 12) - 1) / (0.08/12)

Solving for Monthly Savings:

Monthly Savings = Amount / ((1 + 0.08/12)^(45 * 12) - 1) / (0.08/12)

Substituting the given values:

Monthly Savings = $1,250,000 / ((1 + 0.08/12)^(45 * 12) - 1) / (0.08/12)

Calculating this expression will give us the monthly savings Jennifer needs to make to reach her goal of $1.25 million by age 65.

Answer 2

To retire with $1.25 million at age 65, Jennifer needs to save approximately $286.45 per month starting at age 20, given an annual interest rate of 8%, compounded monthly.

Step-by-step explanation:

Retirement Savings Calculation

To determine how much Jennifer needs to save every month to reach her goal of $1.25 million by age 65, we use the future value of an annuity formula, which considers regular deposits into an account that earns compound interest. Given an average annual interest rate of 8%, we need to find the monthly savings amount that will accumulate to the desired retirement fund over the course of 45 years—since Jennifer is currently 20 years old.

The future value of an annuity formula is:

FV = P * [(
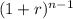`(1 + r)^(n - 1)` / r] where:

• FV is the future value of the annuity
• P is the periodic payment
• r is the periodic interest rate
• n is the number of periods

Using a financial calculator or an algebraic approach, we can solve for P, which is the amount Jennifer needs to save each month. With an 8% annual interest rate compounded monthly, r = 0.08/12 per month, and n = 45 years * 12 months/year, we find:

P = FV / [(
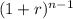`(1 + r)^(n - 1)`) / r]

P = 1,250,000 / [(
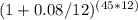`(1 + 0.08/12)^((45*12))` - 1) / (0.08/12)]

After calculations, Jennifer needs to save approximately $286.45 per month for the next 45 years to retire with $1.25 million, assuming an 8% return on investment.