Question

Assume you have taken out a 25 -year loan of $177,390 with an annual interest rate of 6.75%, compounded monthly. (a) Determine the payment amount (in dollars), to the nearest cent, on the given loan amount. 5 (b) Determine the outstanding balance (in dollars), to the nearest dollar, after 17 years.

Answer 1

The monthly payment on the loan is approximately $1,211.89. The outstanding balance after 17 years is approximately $101,381.63.

Step-by-step explanation:

To determine the payment amount on the loan, we can use the formula for the present value of an annuity:

`P = R * (1 - (1 + i)^-^n) / i`

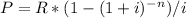
where P is the loan amount, R is the monthly payment, i is the monthly interest rate, and n is the total number of payments. Plugging in the given values, we have:

P = $177,390
i = 0.0675 / 12
n = 25 * 12

Using these values, we can solve for R:

R = $177,390 * (0.005625 / (1 - (1 + 0.005625)⁻³⁰⁰))

R ≈ $1,211.89

Therefore, the monthly payment on the loan is approximately $1,211.89.

To determine the outstanding balance after 17 years, we can use the formula for the future value of an annuity:

`FV = P * ((1 + i)^n ^- ^1) / i`

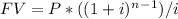
where FV is the future value, P is the loan amount, i is the monthly interest rate, and n is the total number of payments. Plugging in the given values, we have:

P = $177,390
i = 0.0675 / 12
n = 17 * 12

Using these values, we can solve for FV:

FV = $177,390 * ((1 + 0.005625)²⁰⁴⁻¹) / 0.005625

FV ≈ $101,381.63

Therefore, the outstanding balance after 17 years is approximately $101,381.63.