Question

( PLEASE HELP ) X_{1}*X_{2} + X_{2}*X_{3} - X_{3}*X_{4} - X_{4}*X_{5} Let k be a positive integer. If X_{k} = 2/k for any positive value of k, what is the value of the above expression ? A. 64/25 B. 32/15 C. 16/8 D. 8/3

Answer 1

B. 32/15

Explanation:

Given:

`\begin{cases}x_(1)\cdot x_(2) + x_(2)\cdot x_(3) - x_(3)\cdot x_(4) - x_(4)\cdot x_(5)\\\\x_(k) = (2)/(k), \;\;\; k > 0\end{cases}`

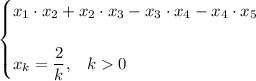
To find the value of the expression given xₖ = 2/k for any positive value of k, substitute xₖ with 2/k for each term:

`x_(1)\cdot x_(2) + x_(2)\cdot x_(3) - x_(3)\cdot x_(4) - x_(4)\cdot x_(5)`

`= (2)/(1)\cdot (2)/(2) + (2)/(2)\cdot (2)/(3) - (2)/(3)\cdot (2)/(4) - (2)/(4) \cdot (2)/(5)`

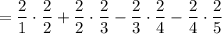
Multiply the fractions:

`= (4)/(2) + (4)/(6)- (4)/(12) - (4)/(20)`

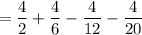
Reduce the fractions to their simplest form:

`= (2)/(1) + (2)/(3)- (1)/(3) - (1)/(5)`

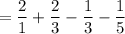
To add and subtract the fractions, they need to have the same denominator. The denominator should be the least common multiple (LCM) of all the denominators. In this case, the LCM is 15. Multiply the numerator and denominator of each fraction by the same number to make the denominator 15:

`= (2 \cdot 15)/(1 \cdot 15) + (2 \cdot 5)/(3\cdot 5)- (1\cdot 5)/(3\cdot 5) - (1\cdot 3)/(5\cdot 3)`

`= (30)/(15)+(10)/(15)-(5)/(15)-(3)/(15)`

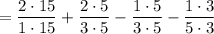
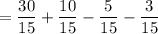
As the denominators of the fractions are now the same, we can simply add and subtract the numerators:

`= (30+10-5-3)/(15)`

`= (32)/(15)`

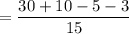
Therefore, the value of the expression is 32/15.