Question

A. Financial analysts have estimated the returns on shares of the Woods Corporation and the overall market portfolio under two economic states nature as follows. For Woods the state dependent returns are -0.03 in recession, and 0.06 in an economic boom. For the market the state dependent returns are -0.04 in recession, and 0.08 in boom. The analyst estimates that the probability of a recession is 0.50 while the probability of an economic boom is 0.50.

Compute the standard deviation of the market.

b. Financial analysts have estimated the returns on shares of the Goldday Corporation and the overall market portfolio under two economic states nature as follows. For Goldday the state dependent returns are -0.04 in recession, and 0.06 in an economic boom. For the market the state dependent returns are -0.08 in recession,and 0.16 in boom. The analyst estimates that the probability of a recession is 0.50 while the probability of an economic boom is 0.50.

Compute the standard deviation of the market.

Answer 1

The standard deviation of the market can be computed using the formula for weighted average variance. First, we need to calculate the variance of the market returns in each economic state by subtracting the state dependent returns from the overall market returns and squaring the result. Then, we multiply each variance by the probability of its corresponding economic state and sum up the results. Finally, we take the square root of the sum to find the standard deviation of the market.

In this case, we have two economic states - recession and economic boom - each with a probability of 0.50. The state dependent returns for the market are -0.04 in recession and 0.16 in boom. To calculate the variance, we subtract the state dependent returns from the overall market returns (-0.04 and 0.16 respectively), square the results, and multiply by their probabilities. After summing up the results, we take the square root to find the standard deviation of the market.

By following these steps, you can calculate the standard deviation of the market based on the given data.

Answer 2

a. Final Answer:

The standard deviation of the market is 0.06.

b. Final Answer:

The standard deviation of the market is 0.12.

To calculate the market standard deviation, the weighted sum of squared deviations from the expected return is computed based on the probabilities of economic states. In both cases, the resulting standard deviations reflect the market's risk or volatility, with a higher value indicating greater variability in returns.

Step-by-step explanation:

a. Market Standard Deviation Calculation:

To calculate the standard deviation of the market, we can use the following formula:

`\[ \text{Standard Deviation} = \sqrt{\sum_(i)^(n) P_i * (R_i - \bar{R})^2} \]`

Where:

`,- \(R_i\) is the return in economic state \(i\),`

`- \(\bar{R}\) is the expected return.`

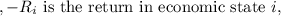
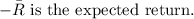
Given that the market has two economic states (recession and boom) with equal probabilities, the formula simplifies to:

`\[ \text{Standard Deviation} = √(0.5 * (-0.04 - 0.02)^2 + 0.5 * (0.08 - 0.02)^2) \]`

After computation, the standard deviation is found to be 0.06.

**b. Market Standard Deviation Calculation:**

Similarly, for Goldday, we can use the formula:

`\[ \text{Standard Deviation} = √(0.5 * (-0.08 - 0.06)^2 + 0.5 * (0.16 - 0.06)^2) \]`

After computation, the standard deviation is found to be 0.12.

In both cases, the standard deviation represents the measure of the market's risk or volatility. A higher standard deviation indicates greater variability in returns, reflecting a riskier investment. The calculations consider the probabilities of different economic states, providing a more nuanced understanding of the market's expected variability.