Question

( PLEASE HELP ) 3 eggs and 4 strips of bacon cost $3.10 . 5 eggs and 1 strip of bacon cost $4.90 . If a family orders 16 eggs and 10 strips of bacon , how much , in dollars , do they pay ?

Answer 1

$16.02 ≈ $16

Explanation:

Let x be the cost of one egg.

Let y be the cost of one strip of bacon.

According to the given information, we can create the following system of equations:

`3x + 4y = 3.10`

`5x + y = 4.90`

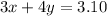
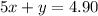
Rearrange the second equation to isolate y:

`\begin{aligned}5x + y &= 4.90\\5x + y -5x&= 4.90-5x\\y&=4.90-5x\end{aligned}`

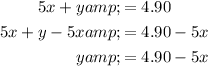
Substitute this into the first equation and solve for x:

`\begin{aligned}3x + 4y &= 3.10\\3x+4(4.90-5x)&=3.10\\3x+19.60-20x&=3.10\\19.60-17x&=3.10\\19.60-3.10&=17x\\16.50&=17x\\x&=0.970588...\\x&=0.97\; \sf(nearest\;hundredth)\end{aligned}`

Therefore, the cost of one egg is $0.97 (rounded to the nearest cent).

To find the cost of one strip of bacon (y), substitute the found value of x into the rearranged second equation and solve for y:

`\begin{aligned}y&=4.90-5x\\y&=4.90-5(0.970588...)\\y&=4.90-4.852941...\\y&=0.0470588...\\y&=0.05\; \sf (nearest\;hundredth)\end{aligned}`

Therefore, the cost of one strip of bacon is $0.05 (rounded to the nearest cent).

To calculate how much it would cost for 16 eggs and 10 strips of bacon, substitute the found values of x and y into the equation 16x + 10y:

`\begin{aligned}\sf 16\;eggs+10\;bacon&=16x+10y\\&=16(0.97)+10(0.05)\\&=15.52+0.50\\&=16.02\end{aligned}`

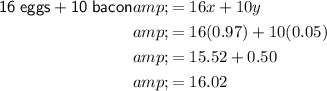
Therefore, it would cost $16.02 (rounded to the nearest cent), or $16 (rounded to the nearest dollar) to buy 16 eggs and 10 strips of bacon.