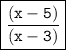Question

Please help cannot figure this out

Answer 1

x-5/x-3

Explanation:

First, factor f(x) and g(x).

f(x)=
`x^(2)`-x-20

`x^(2)`+4x-5x-20

x(x+4)-5(x+4)

(x+4) (x-5)

g(x)=
`x^(2)`+x-12

`x^(2)`+4x-3x-12

x(x+4)-3(x+4)

(x+4)(x-3)

Second, you must divide f(x) and g(x), since f/g.

(x+4)(x-5) / (x+4)(x-3)

Lastly, since (x+4) cancels out

x-5/x-3

Answer 2

`\boxed{\tt ((x - 5) )/((x - 3))}`

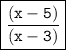
Explanation:

Given:

f(x) =x^2-x-20

g(x)=x^2+x-12

To find: f/g

Solution:

We can find f/g by dividing the expressions for f(x) and g(x). The quotient is:

`\tt (f(x) )/(g(x) )= ((x^2 - x - 20) )/((x^2 + x - 12))`

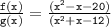
We can factor the expressions in the numerator and denominator to simplify the quotient. The numerator can be factored as:

`\tt x^2 - x - 20`

doing middle-term factorization

`\tt x^2-(5-4)x -20`

`\tt x^2 -5x+4x-20`

`\tt x(x-5)+4(x-5)`

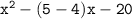
(x + 4)(x - 5)

The denominator can be factored as:

`\tt x^2 + x - 12`

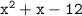
doing middle-term factorization

`\tt x^2 +(4-3)x -12`

`\tt x^2 +4x -3x -12`

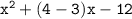
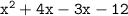
x(x+4)-3(x+4)

(x + 4)(x - 3)

Substituting the factored expressions into the quotient, we get:

`\tt (f(x))/(g(x)) =((x + 4)(x - 5) )/( (x + 4)(x - 3))`

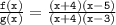
The factors of x + 4 cancel out, leaving us with:

`\tt (f(x))/(g(x)) = ((x - 5) )/((x - 3))`

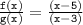
Therefore, the simplified expression for f/g is
`\boxed{\tt ((x - 5) )/((x - 3))}`