Question

Consumers' and Producers' Surplus

The management of the Titan Tire Company has determined that the quantity demanded x of their Super Titan tires/week is related to the unit price p by the relation
p = 132 − x2
where p is measured in dollars and x is measured in units of a thousand. Titan will make x units of the tires available in the market if the unit price is
p = 36 + 1/2x2
dollars. Determine the consumers' surplus and the producers' surplus when the market unit price is set at the equilibrium price. (Round your answers to the nearest dollar.)
consumer's surplus $
producer's surplus $

Answer 1

To find the equilibrium quantity and price from the given demand and supply equations, solve for x by equating the demand and supply functions. Then, use the equilibrium quantity and price to calculate the areas of consumer surplus and producer surplus. The consumer surplus is $128,000, and the producer surplus is $256,000 after rounding.

Step-by-step explanation:

In determining the consumer surplus and producer surplus, we first need to find the equilibrium price where demand equals supply. From the given equations p =
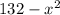`132 - x^(2)` for demand and p = 36 +
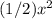`(1/2)x^(2)` for supply, setting them equal, we have 132 -
`x^(2)` = 36 +
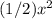`(1/2)x^(2)`, which simplifies to 3/2 x2 = 96, yielding
`x^(2)` = 64 and x=8 when solved for the positive quantity. Hence, the equilibrium quantity is 8,000 units (as x is in thousands of units), and the equilibrium price p is $100, found by substituting x back into either the demand or supply equation.

To find the consumer's surplus, we calculate the area above the price level of $100 and below the demand curve from 0 to 8,000 units, which is a triangle with the height of 132 - 100 = 32 and the base of 8,000 units, giving a surplus of (1/2)*8,000*32, which is $128,000 after rounding. Similarly, the producer's surplus is the area below the price level of $100 and above the supply curve from 0 to 8,000 units, which is a triangle with the height of 100 - 36 = 64 and the base of 8,000 units, resulting in a surplus of (1/2)*8,000*64, which is $256,000 after rounding.