Question

Use an interval of 0.001 to determine the instantaneous rate of change of the function (z) = 3z 3 − 12z 2 + z − 2 z at z = −3. (z) is measured in dollars, and z is measured in pages. Give your answer to the nearest tenth.

Answer 1

The instantaneous rate of change of the function at z = -3 can be calculated using the limit definition of the derivative by finding the average rate of change over an interval of 0.001 and then rounding the result to the nearest tenth.

Step-by-step explanation:

To find the instantaneous rate of change of the function at z = -3 using an interval of 0.001, we will use the limit definition of the derivative. Unfortunately, the question contains a typo in the function (z). Assuming the correct function is f(z) = 3z^3 - 12z^2 + z - 2, we will proceed with the calculation.

The instantaneous rate of change at z = -3 is approximated by the average rate of change between z = -3 and z = -3.001, which can be calculated as:

f'(-3) ≈ [f(-3.001) - f(-3)] / (-3.001 + 3)

Calculating each function value:

f(-3) = 3(-3)^3 - 12(-3)^2 + (-3) - 2

• 
  
• And then calculating the difference quotient:

f'(-3) ≈ [f(-3.001) - f(-3)] / 0.001

Finally, we round the resulting rate of change to the nearest tenth as requested.

Answer 2

The rate of change of the function
`\( g(z) \)` at
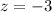`\( z = -3 \)`, to the nearest tenth, is 154.0.

The instantaneous rate of change of the function
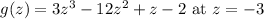`\( g(z) = 3z^3 - 12z^2 + z - 2 \) at \( z = -3 \)` can be found by taking the derivative of
`\( g(z) \)` with respect to
`\( z \)` and evaluating it at
`\( z = -3 \)`.

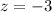The derivative of
`\( g(z) \)`, denoted as
`\( g'(z) \)`, is
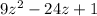`\( 9z^2 - 24z + 1 \)`. Evaluating this at
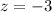`\( z = -3 \)` gives us the instantaneous rate of change:

`\[ g'(-3) = 9(-3)^2 - 24(-3) + 1 = 154 \]`

This is the exact value of the instantaneous rate of change at
`\( z = -3 \)`.

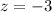However, to approximate this value using an interval of 0.001, we calculate the average rate of change between
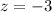`\( z = -3 \)` and
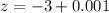`\( z = -3 + 0.001 \)`. This gives us an approximate value of:

`\[ (g(-3 + 0.001) - g(-3))/(0.001) \approx 153.961 \]`

Rounded to the nearest tenth, the approximate instantaneous rate of change is 154.0 (since the exact and the approximate values are very close, the rounding doesn't change the result).

Therefore, The answer is 154.0.