Question

Find an equation of the tangent line to the curve defined parametrically by x=t³−t and y=t⁴−3t²+3 at t=2

Answer 1

Explanation:

Firstx let find the coordinate point, plug in 2 for t into each functions

`x(2) = 2 {}^(3) - 2 = 6`

`y(2) = 2 {}^(4) - 3(2) {}^(2) + 3 = 7`

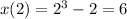
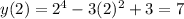
So the coordinate pair is (6,7)

Given the functions

`x(t)`

and

`y(t)`

`(dy)/(dx) = ( (dy)/(dt) )/( (dx)/(dt) )`

Take the derivative of the y function first

`(dy)/(dt) = 4t {}^(3) - 6t`

`(dx)/(dt) = 3 {t}^(2) - 1`

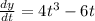
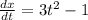
So

`(dy)/(dx) = \frac{2t( 2{t {}^(2) } - 3)}{3 {t}^(2) - 1}`

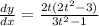
Plug in x=2 into the day/dx to find the tangential slope

`(dy)/(dx) (2) = \frac{2(2)((2 * {2}^(2) - 3 )}{3(2) {}^(2) - 1} = (4(5)/(11) = (20)/(11)`

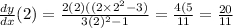
We know it passes through (6,7) so

`y = 7 + (20)/(11) (x - 6)`

Or simplified

`y = (20)/(11) x + (43)/(11)`