Question

What point on the line y=3x+6 is closest to the origin?

The point on the line y=3x+6 closest to the origin is □.
(Type an ordered pair. Simplify your answer. Type integers or simplified fractions.)

Answer 1

The point on the line y=3x+6 closest to the origin is (0,2).

Step-by-step explanation:

The point on the line y=3x+6 closest to the origin is (0,2).

To find the point on the line that is closest to the origin, we need to find the point that has the shortest distance from the origin. The origin is represented by the point (0,0), so we need to find the point on the line that is closest to this origin point.

Since the equation of the line is y=3x+6, we can substitute x=0 into the equation to find the y-coordinate. When x=0, y=3(0)+6=6. Therefore, the point on the line that is closest to the origin is (0,6).

Answer 2

The point on the line y=3x+6 closest to the origin is (-2/3, 2).

Step-by-step explanation:

To find the point on the line y=3x+6 that is closest to the origin, we need to find the distance between the origin and any point on the line. The distance between two points (x1, y1) and (x2, y2) can be calculated using the distance formula:

`d = \sqrt{(x2-x1)^2 + (y2-y1)^2)`

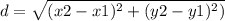
In this case, the origin corresponds to the point (0, 0). Substituting the equation of the line into the distance formula, we get:

`d = \sqrt{(x^2 + (3x+6)^2)`

To find the minimum distance, we can find the minimum of this function. We can do this by finding the x-coordinate that minimizes the function, since the x-coordinate determines the y-coordinate on the line.

By plotting the function or by using calculus, we can find that the minimum distance occurs when x = -2/3. Plugging this value back into the equation of the line, we get:

(-2/3, 2)