Question

Using Descartes' Rule of Signs, determine the possible number of positive real zeros and the possible number of negative real zeros of the polynomial function \[ f(x)=-2 x^{4}+3 x^{3}-5 x^{2}+4 x-1 \]

Answer 1

4, 2, or 0 positive real zeroes

0 negative real zeroes

Explanation:

Descartes' Rule of Signs says that the number of positive real zeroes are determined by observing the number of sign changes in f(x), and same goes for negative real zeroes for f(-x):

`f(x)=-2x^4+3x^3-5x^2+4x-1`

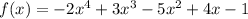
We can see there are 4 sign changes in f(x), so there are either 4, 2, or 0 positive real zeroes.

`f(-x)=-2(-x)^4+3(-x)^3-5(-x)^2+4(-x)-1\\f(-x)=-2x^4-3x^3-5x^2-4x-1`

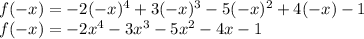
We can see there are 0 sign changes in f(x), so there are 0 negative real zeroes.