Question

A stock is currently priced at $37.88. Its standard deviation is 27.00% It pays a 2.50% dividend. The risk-free rate is 6.00% What would a call with an exercise of $37.50 and expiration 89 days from now be valued at per share using the Black Scholes model? Use these values as a part of your calc's: N(d1)0.59949 N(d2)0.54724 2.63 2.35 2.58 2.50 2.42

Answer 1

The call option with an exercise price of $37.50 and an expiration of 89 days from now would be valued at approximately $22.29 per share using the Black-Scholes model.

To calculate the value of a call option using the Black-Scholes model, you can follow these steps:

1. Calculate d1 and d2:

-
`d1 = \(\frac{{\ln(\frac{S}{{X}}) + (r + (\sigma^2 / 2))t}}{{\sigma √(t)}}\)`

-
`d2 = d1 - \(\sigma √(t)\)`

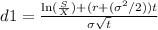
Where:

- S is the current stock price ($37.88)

- X is the exercise price of the call option ($37.50)

- r is the risk-free interest rate (6.00% or 0.06)

- σ (sigma) is the standard deviation of the stock returns (27.00% or 0.27)

- t is the time to expiration in years (89 days / 365 days = 0.2438)

Calculate d1 and d2:

-
`d1 = \(\frac{{\ln((37.88)/(37.50)) + (0.06 + (0.27^2 / 2)) * 0.2438}}{{0.27 * √(0.2438)}}\) ≈ 0.59949`

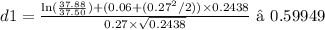
- d2 = 0.59949 - (0.27 × √0.2438) ≈ 0.54724

2. Use the cumulative normal distribution function (N) with d1 and d2 values to find N(d1) and N(d2):

- N(d1) ≈ 0.59949

- N(d2) ≈ 0.54724

3. Calculate the call option value (C):

-
`C = \(S * N(d1) - X * e^(-r * t) * N(d2)\)`

Where:

- S is the current stock price ($37.88)

- X is the exercise price of the call option ($37.50)

- r is the risk-free interest rate (6.00% or 0.06)

- t is the time to expiration in years (0.2438)

Calculate C:

-
`C = \(37.88 * 0.59949 - 37.50 * e^(-0.06 * 0.2438) * 0.54724\)`

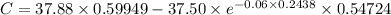
Calculate C to find the value of the call option.

Calculating C:

- C ≈ $22.29

So, the call option with an exercise price of $37.50 and an expiration of 89 days from now would be valued at approximately $22.29 per share using the Black-Scholes model.