Question

This is the graph of f(x)=(x+A)/(x+B). The grid lines in the graph are one unit apart.

What is the value of A/B?

P.S.: There is already the same question posted, but the answer is wrong. Please explain clearly!

Answer 1

A/B = -2

Explanation:

Given rational function:

`f(x)=(x+A)/(x+B)`

The given diagram is a graph of the given rational function f(x) with a vertical asymptote at x = 1 and a horizontal asymptote at y = 1.

The vertical asymptote(s) of a rational function occur at the x-value(s) that make the denominator of the function zero.

Therefore, to find the value of B, set the denominator to zero, substitute x = 1, and solve for B:

`\begin{aligned}x+B&=0\\1+B&=0\\1+B-1&=0-1\\B&=-1\end{aligned}`

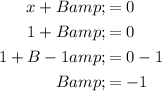
Therefore, the value of B is -1.

From inspection of the graph, we can see that the function passes through the point (0, -2).

To find the value of A, substitute the point (0, -2) and the found value of B = -1 into the rational function and solve for A:

`\begin{aligned}(x+A)/(x+B)&=y\\\\(0+A)/(0-1)&=-2\\\\ (A)/(-1)&=-2\\\\(A)/(-1) \cdot (-1)&=-2\cdot (-1)\\\\A&=2\end{aligned}`

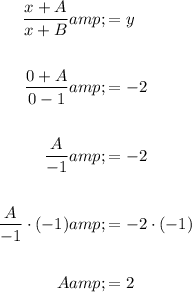
Therefore, the value of A is 2.

Finally to find the value of A/B, divide the found values of A and B:

`(A)/(B)=(2)/(-1)=-2`

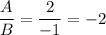
Therefore, the value of A/B is -2.