Question

A 400 N box is resting on a 25 degree incline. The coefficient of static friction is 0.35. Find the maximum and minimum values of an applied force, P, for which the block is in equilibrium.

Answer 1

Approximately
`42.2\; {\rm N}` and approximately
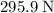`295.9\; {\rm N}`, assuming that the applied force points upward along the slope and that the box is stationary.

Step-by-step explanation:

To find the maximum and minimum values of the applied force, start by analyzing all the forces on the box in this question and find an expression for friction in terms of the applied force. Make use of the coefficient of static friction to construct an inequality bounding the magnitude of friction. To find the maximum and minimum values of the applied force on the box, rewrite the inequality on friction into an inequality bounding this applied force.

Refer to the diagram attached (not to scale.) Forces on this box include the following:

• Weight
  `m\, g = 400\; {\rm N}`, vertically downward.
• Normal force, upward along the slope.
• The applied force.
• Friction, which might point either upward along the slope, downward along the slope, or be
  `0` in some cases.

Let
`\theta = 25^(\circ)` denote the incline of this slope. Decompose forces on this box in two orthogonal components: perpendicular to the slope and along the slope. This decomposition helps make use of fact that forces in the component perpendicular to the slope must always be balanced.

Forces in the component perpendicular to the slope include:

• Component of weight perpendicular to the slope:
  `m\, g\, \cos(\theta)` (into the slope.)
• Normal force on the box is entirely in this component (pointing out of the slope.)

Forces in the component along the slope include:

• Component of weight along the slope:
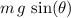  `m\, g\, \sin(\theta)` (along the slope and downward.)
• Friction.
• Applied force (along the slope and upward under the assumptions.)

Forces in the component perpendicular to the slope must be balanced. Hence, the normal force on this box needs to be equal in magnitude (but opposite in direction) to the component of weight perpendicular to the slope. In other words:

`(\text{normal force}) = m\, g\, \cos(\theta)`.

Assuming that the box isn't moving, the maximum possible magnitude of friction depends on the normal force and the coefficient of static friction,
`\mu_{\text{s}}`:

`(\text{friction}) \le (\mu_{\text{s}})\, (\text{normal force})`.

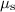When friction is in the opposite direction (downward along the slope,) the sign in front this force would be negative. Accordingly, the inequality would become:

`(\text{friction}) \ge - (\mu_{\text{s}})\, (\text{normal force})`.

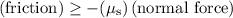These equations bound the magnitude of the static friction on this box.

For the box to be stationary, forces on the box should be balanced not just perpendicular to the slope, but also along the slope. In other words:

`(\text{friction}) + (\text{applied force}) - m\, g\, \sin(\theta) = 0`.

Note that while weight points downward along the slope, the applied force points upward along the slope. Hence, the sign in front of the weight component should be negative while the sign in front the applied force should be positive.

Rearrange this equation to find an expression for static friction:

`(\text{friction}) = m\, g\, \sin(\theta) - (\text{applied force})`.

Substitute the expression above into the inequalities that bound the magnitude of friction:

`m\, g\, \sin(\theta) - (\text{applied force}) \le (\mu_{\text{s}})\, (\text{normal force})`.

`m\, g\, \sin(\theta) - (\text{applied force}) \ge -(\mu_{\text{s}})\, (\text{normal force})`.

Rearrange these inequalities to bound the applied force on the box:

`(\text{applied force}) \ge m\, g\, \sin(\theta) - (\mu_{\text{s}})\, (\text{normal force})`.

`(\text{applied force}) \le m\, g\, \sin(\theta) + (\mu_{\text{s}})\, (\text{normal force})`.

Since
`(\text{normal force}) = m\, g\, \cos(\theta)` from a previous step, these inequalities become:

`(\text{applied force}) \ge m\, g\, \sin(\theta) - \mu_{\text{s}}\, m\, g\, \cos(\theta)`.

`(\text{applied force}) \le m\, g\, \sin(\theta) + \mu_{\text{s}}\, m\, g\, \cos(\theta)`.

Substitute
`m\, g = 400\; {\rm N}`,
`\theta = 25^(\circ)`, and
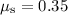`\mu_{\text{s}} = 0.35` into the inequalities to obtain:

`(\text{applied force}) \ge 42.2\; {\rm N}` (rounded up.)

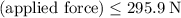`(\text{applied force}) \le 295.9\; {\rm N}` (rounded down.)

Note that the lower bound on this applied force is positive, meaning that the upward push is necessary. Without this force, the static friction on the box would not be sufficient to prevent the box from sliding down.