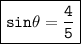Question

30 POINTS!

Find the exact value of sin space theta, where theta is the angle shown. Simplify.

(Im not sure if that makes sense but theta is 0 with a line in the middle)

Answer 1

sinθ =
`(4)/(5)`

Explanation:

before calculating sinθ we require to find the value of b

using Pythagoras' identity in the right triangle

b² + 9² = 15²

b² + 81 = 225 ( subtract 81 from both sides )

b² = 144 ( take square root of both sides )

b =
`√(144)` = 12 = AC

Then

sinθ =
`(opposite)/(hypotenuse)` =
`(AC)/(AB)` =
`(12)/(15)` =
`(4)/(5)`

Answer 2

`\boxed{\tt sin \theta = (4)/(5)}`

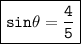
Explanation:

In right angled triangle Δ ACB with respect to θ or ∡B

Perpendicular = AC=b

Base=BC=9

Hypotenuse=AB=15

By using Pythagoras' theorem,

`\boxed{ \tt Hypotenuse^2=Base^2+Perpendicular^2}`

`\tt AB^2=BC^2+AC^2`

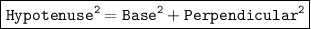
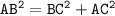
substituting value

`\tt 15^2=9^2+b^2`

`\tt b^2=15^2-9^2`

`\tt b^2=144`

`\tt b=√(144)`

`\tt b=12`

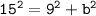
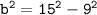
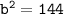
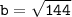
Again,

We have

`\boxed{\tt sin\theta = (Perpendicular )/(Hypotenuse)}`

`\tt sin \theta = (AC)/(AB)`

`\tt sin \theta = (b)/(15)`

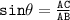
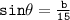
substituting the value of b.

`\tt sin \theta = (12)/(15)`

while reducing

`\tt sin \theta = (4)/(5)`

Therefore, answer is the second option
`\boxed{\tt sin \theta = (4)/(5)}`