Answer:
CA = 34.
Explanation:
Given:
ΔBDC and ΔADC are right-angled triangles
In ΔBDC with respect to ∡B
Base = BD = 12
Hypotenuse =BC= 20
Perpendicular = CD
Let's find the length of CD by using Pythagoras' theorem
We have:
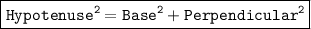
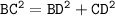
substituting value
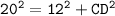
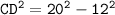
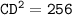
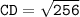
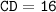

Again,
In ΔADC with respect to ∡A
Base = AD= 30
Hypotenuse =AC
Perpendicular =CD=16
Let's find the length of AC which is hypotenuse by using Pythagoras' theorem
We have:
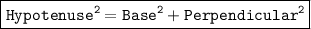
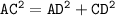
substituting value
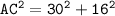
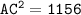
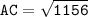
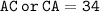
Therefore, the length of segment CA is 34.