Question

Find mzCAB.

B
H
DC
(4x+23)
Algebra Einstein, 2023
(11x-33)°
A
E
G
F

Answer 1

Hello!

Answer:

`\Large \boxed{\sf CAB = 55^(\circ)}`

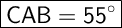
Step-by-step explanation:

We know that DE // BF

So the angles ACE and CAB are alternate interior.

So ACE = CAB.

Therefore, we have the equation:

`\sf 11x - 33 = 4x + 23`

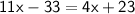
For find CAB, we must find the value of x.

So, solve the equation:

`\sf 11x - 33 = 4x + 23`

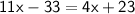
◼ Subtract 4x from both sides:

`\sf 11x - 33-4x = 4x + 23 -4x`

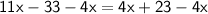
◼ Simplify the sides:

`\sf 7x - 33 = 23`

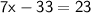
◼ For isolate x, go add 33 from both sides:

`\sf 7x - 33 +33= 23 +33`

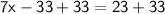
◼ Simplify the sides:

`\sf 7x = 56`

◼ Divide both sides by 7:

`\sf (7x)/(7) = (56)/(7)`

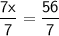
◼ Simplify the sides:

`\sf x = 8`

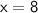
The angles CAB is equal to:

◼ Go replace x by 8 in CAB:

`\sf CAB = 4 * 8 + 23`

◼ Simplify the result:

`\sf CAB = \boxed{\sf 55^(\circ)}`

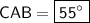
Go check if the equality CAB = ACE is respected:

`\sf ACE = 11 * 8- 33`

◼ Simplify the result:

`\sf CAB = \boxed{\sf 55^(\circ)}`

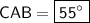
So the check is good.

Answer 2

• 
  `\sf m\angle CAB` is 55°

Step-by-step Step-by-step explanation:

From the given Figure ,

`\sf m\angle CAB` = (4x + 23)°

`\sf m\angle ACE` = (11x - 33)°

`\sf m\angle CAB` and
`\sf m\angle ACE` are the alternate angles.

Since we know that when any two lines cut by transversal, then the measure of the alternate angles is always equal.

So
`\sf m\angle CAB` =
`\sf m\angle ACE`

`\sf 4x + 23 = 11x - 33`

Move all the terms containing x to the left side and others to the right side

`\sf 4x - 11x = -33 - 23`

`\sf - 7x = -56`

Divide both sides by -7,

`\sf x = 8`

Since
`\sf m\angle CAB` = (4x + 23)°

Plugging the value of x here,

`\sf m\angle CAB` = (4*8 + 23)

`\sf m\angle CAB` = 32 + 23

`\sf m\angle CAB` = 55°

Henceforth, the value of
`\sf m\angle CAB` is 55°