Question

Consider the surface

S
which is the part of the plane
z=x+y
above the unit square
0≤x≤1,0≤y≤1
Find the flux of
(z,x,y)

Answer 1

The flux of the vector field (z,x,y) across the surface S is −1.

Let's go through the calculation again to find the flux of the vector field (z, x, y) across the surface S, where S is the part of the plane z=x + y above the unit square 0≤x≤1, 0≤y≤1.

We want to find:

`\text { Flux }=\iint_S \mathbf{F} \cdot d \mathbf{S}`

where F=(z, x, y) and dS is the outward-pointing normal vector to the surface S.

Parameterize the Surface:

`\mathbf{r}(x, y)=(x, y, x+y)`

Compute Partial Derivatives:

`\frac{\partial \mathbf{r}}{\partial x}=(1,0,1)`

Compute the Cross Product:

`d \mathbf{S}=\frac{\partial \mathbf{r}}{\partial x} * \frac{\partial \mathbf{r}}{\partial y}=(-1,-1,1) .`

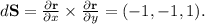
Compute the Flux:

`\text { Flux }=\iint_S \mathbf{F} \cdot d \mathbf{S}=\iint_S(-(x+y)-x+y) d S`

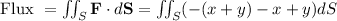
Now, integrate over the unit square:

`\begin{aligned}& \text { Flux }=\int_0^1 \int_0^1(-2 x) d y d x \\& =\int_0^1[-2 x y]_0^1 d x \\& =\int_0^1(-2 x) d x \\& =\left[-x^2\right]_0^1 \\& =-1-(0) \\& =-1 .\end{aligned}`

Question:

Consider the surface S which is the part of the plane z= x + y, above the unit square 0≤x≤1, 0≤y≤1. Find the flux of (z, x, y).