Question

The function f is defined by f: x4 sin x-1 for -1/2π x< 1/2 π

(i) State the range of f.
(ii) Find the coordinates of the points at which the curve y = f(x) intersects the coordinate axes.
(iii) Sketch the graph of y = f(x).
(iv) Obtain an expression for f-¹(x), stating both the domain and range of f-1.

Answer 1

`\textsf{(i)}\quad -5 \leq f(x) \leq 3`

`\textsf{(ii)}\quad (0, -1), \;(0.2527, 0)`

`\textsf{(iii)}\quad \sf See \;attachment.`

`\textsf{(iv)}\quad f^(-1)(x)=\arcsin\left((x+1)/(4)\right)`

`\textsf{Domain:}\quad -5 \leq x \leq 3`

`\textsf{Range:}\quad -(1)/(2)\pi \leq x \leq (1)/(2)\pi`

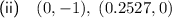
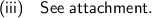
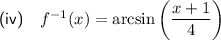
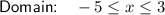
Explanation:

The function f is defined by:

`f(x) = 4\sin(x) - 1\:,\quad \textsf{for}\;-(1)/(2)\pi \leq x \leq (1)/(2)\pi`

`\hrulefill`

Part (i)

To determine the range of function f(x), we need to find the set of all possible x-values that f(x) can take.

Since -1 ≤ sin(x) ≤ 1, the range of 4sin(x) will be -4 ≤ 4sin(x) ≤ 4.

Subtracting 1 from this range, the range of f(x) is:

`\boxed{-5 \leq f(x) \leq 3}`

`\hrulefill`

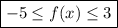
Part (ii)

To find the coordinates of the point at which the curve y = f(x) intersects the y-axis, substitute x = 0 into the function:

`\begin{aligned}x=0 \implies f(0)&=4\sin(0) - 1\\&=4(0)-1\\&=0-1\\&=-1\end{aligned}`

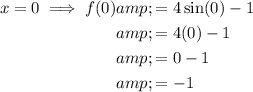
Therefore, the y-intercept is (0, -1).

To find the coordinates of the point at which the curve y = f(x) intersects the x-axis, we need to determine the values of x where f(x) = 0 in the given restricted domain.

`\begin{aligned}f(x)&=0\\4\sin(x) - 1&=0\\4\sin(x)&=1\\\sin(x)&=(1)/(4)\\\\x&=\arcsin\left((1)/(4) \right)+2\pi n\\x&=\pi -\arcsin\left((1)/(4) \right)+2\pi n \end{aligned}`

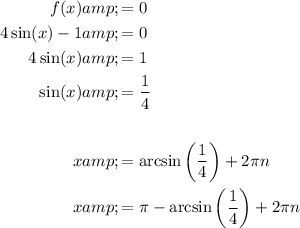
The value of x that satisfies this equation (considering the restricted domain) is:

`x=\arcsin\left((1)/(4) \right)\approx 0.2527\; (4\; \sf d.p.)`

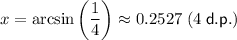
Therefore, the point at which the curve y = f(x) intersects the x-axis in the restricted domain is:

`(0.2527, 0)`

`\hrulefill`

Part (iii)

To sketch the graph of y = f(x), draw the mid-line at y = -1.

Place the minimum points at (-π/2±2πn, -5) and the maximum points at (π/2±2πn, 3).

Draw a smooth sinusoidal curve through the points, ensuring the curve crosses the y-axis at (0, -1) and the x-axis at (0.2527, 0).

`\hrulefill`

Part (iv)

To find the inverse of f(x), begin by swapping x and y:

`x=4\sin(y) - 1`

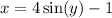
Now, solve for x:

`\begin{aligned}x&=4\sin(y) - 1\\\\x+1&=4 \sin(y)\\\\\sin(y)&=(x+1)/(4)\\\\y&=\arcsin\left((x+1)/(4)\right)\end{aligned}`

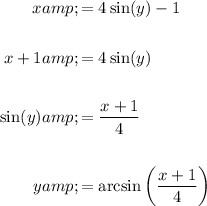
Therefore, the inverse of the function is:

`f^(-1)(x)=\arcsin\left((x+1)/(4)\right)`

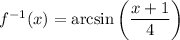
The domain of f⁻¹(x) is the range of f(x), which is -5 ≤ x ≤ 3.

The range of f⁻¹(x) is the domain of f(x), which is -π/2 ≤ f⁻¹(x) ≤ π/2.