Question

Problem 7 (S8). Using only the definition of Riemann sum and your knowledge of limits, compute the exact area under the curve x 2 +x 3

between x=1 and x=3.

Answer 1

The exact area under the curve
`\(x^2 + x^3\)` between x=1 and x=3 is
`\((86)/(3)\)`.

The Riemann sum is given by the sum of the areas of rectangles formed by partitioning the interval [1, 3] and evaluating the function at certain points within each subinterval.

Let's denote Δx as the width of each subinterval. The Riemann sum is then the sum of f(x_i) * Δx for each subinterval.

For the function
`\(f(x) = x^2 + x^3\)`, we have:

`\[ \text{Riemann sum} = \sum_(i=1)^(n) (x_i^2 + x_i^3) \cdot \Delta x \]`

To compute the exact area, we need to take the limit as the number of subintervals (\(n\)) approaches infinity. This limit is expressed as a definite integral:

`\[ \text{Area} = \lim_(n \to \infty) \sum_(i=1)^(n) (x_i^2 + x_i^3) \cdot \Delta x \]`

To simplify further, we can integrate the function over the interval [1, 3]:

`\[ \text{Area} = \int_(1)^(3) (x^2 + x^3) \,dx \]`

Evaluating this integral will give the exact area under the curve between x=1 and x=3.

Let's evaluate the definite integral:

`\[ \text{Area} = \int_(1)^(3) (x^2 + x^3) \,dx \]`

To find the antiderivative, we integrate each term separately:

`\[ \int x^2 \,dx = (1)/(3)x^3 \]`

`\[ \int x^3 \,dx = (1)/(4)x^4 \]`

Now, applying the Fundamental Theorem of Calculus:

`\[ \text{Area} = \left[(1)/(3)x^3 + (1)/(4)x^4\right]_(1)^(3) \]`

Now, substitute the upper limit (3) and lower limit (1) into the antiderivative and subtract:

`\[ \text{Area} = \left((1)/(3)(3)^3 + (1)/(4)(3)^4\right) - \left((1)/(3)(1)^3 + (1)/(4)(1)^4\right) \]`

Calculating this expression will give you the exact area under the curve
`\(x^2 + x^3\)` between x=1 and x=3.

Let's calculate the expression:

`\[ \text{Area} = \left((1)/(3)(3)^3 + (1)/(4)(3)^4\right) - \left((1)/(3)(1)^3 + (1)/(4)(1)^4\right) \]`

`\[ \text{Area} = \left((1)/(3)(27) + (1)/(4)(81)\right) - \left((1)/(3)(1) + (1)/(4)(1)\right) \]`

`\[ \text{Area} = \left(9 + 20.25\right) - \left((1)/(3) + (1)/(4)\right) \]`

`\[ \text{Area} = 29.25 - \left((7)/(12)\right) \]`

Now, find a common denominator for the subtraction:

`\[ \text{Area} = (351)/(12) - (7)/(12) \]`

Combine the fractions:

`\[ \text{Area} = (344)/(12) \]`

Simplify the fraction:

`\[ \text{Area} = (86)/(3) \]`

So, the exact area under the curve
`\(x^2 + x^3\)` between x=1 and x=3 is
`\((86)/(3)\)`.

Answer 2

The exact area under the curve
`x^2+x^3` between x=1 and x=3 is approximately 28.67.

To compute the area under the curve
`x^2+x^3` between x=1 and x=3 using a Riemann sum, we'll set up the integral using a partition of the interval [1,3] into n subintervals.

The width of each subinterval, denoted as Δx, is given by:

`\Delta x=(3-1)/(n)=(2)/(n) .\\`

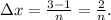
Choose sample points
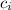`c_(i)` within each subinterval. A common choice is the right endpoint of each subinterval. So,
`c_i=1+i \cdot (2)/(n) \text { for } i=1,2, \ldots, n`

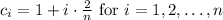
Now, the Riemann sum is given by:

`S=\sum_(i=1)^n f\left(c_i\right) \Delta x_i=\sum_(i=1)^n\left(c_i^2+c_i^3\right) \Delta x_i .`

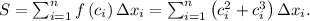
Substitute the expressions for
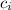`c_(i)` and Δ
`x_(i)` :

`S=\sum_(i=1)^n\left(\left(1+i \cdot (2)/(n)\right)^2+\left(1+i \cdot (2)/(n)\right)^3\right) \cdot (2)/(n)`

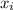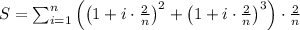
Now, take the limit as n approaches infinity:

`A=\lim _(n \rightarrow \infty) \sum_(i=1)^n\left(\left(1+i \cdot (2)/(n)\right)^2+\left(1+i \cdot (2)/(n)\right)^3\right) \cdot (2)/(n)`

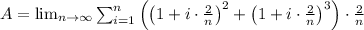
This limit represents the exact area under the curve
`x^2+x^3` between x=1 and x=3 using the Riemann sum approach. To obtain the numerical value, we need to evaluate this limit.

Let's proceed with the evaluation. We'll start by simplifying the Riemann sum:

`S=\lim _(n \rightarrow \infty) \sum_(i=1)^n\left(\left(1+i \cdot (2)/(n)\right)^2+\left(1+i \cdot (2)/(n)\right)^3\right) \cdot (2)/(n)`

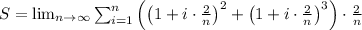
Expand the terms inside the summation:

`S=\lim _(n \rightarrow \infty) \sum_(i=1)^n\left(1+(4 i)/(n)+(4 i^2)/(n^2)+1+(6 i)/(n)+(12 i^2)/(n^2)+(8 i^3)/(n^3)\right) \cdot (2)/(n)`

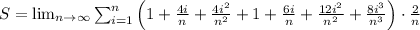
Combine like terms:

`S=\lim _(n \rightarrow \infty) \sum_(i=1)^n\left((6 i^3)/(n^3)+(16 i^2)/(n^2)+(10 i)/(n)+2\right) \cdot (2)/(n)`

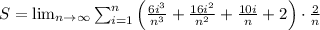
Now, distribute the 2/n :

`S=\lim _(n \rightarrow \infty) \sum_(i=1)^n\left((12 i^3)/(n^4)+(32 i^2)/(n^3)+(20 i)/(n^2)+(4)/(n)\right)`

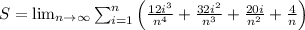
This Riemann sum represents the area under the curve
`x^2+x^3` between x=1 and x=3. Now, let's evaluate the limit:

`A=\lim _(n \rightarrow \infty) \sum_(i=1)^n\left((12 i^3)/(n^4)+(32 i^2)/(n^3)+(20 i)/(n^2)+(4)/(n)\right) .`

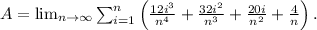
This limit is a Riemann sum that tends toward the definite integral:

`A=\int_1^3\left(x^2+x^3\right) d x`

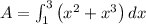
Now, let's integrate:

`A=\left[(1)/(3) x^3+(1)/(4) x^4\right]_1^3 \text {. }`

Evaluate at the upper and lower limits:

`A=\left((1)/(3)(3)^3+(1)/(4)(3)^4\right)-\left((1)/(3)(1)^3+(1)/(4)(1)^4\right) .`

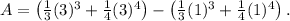
Calculate the values:

`A=(9+20.25)-\left((1)/(3)+(1)/(4)\right)`

`A=29.25-\left((4+3)/(12)\right)`

`A=29.25-(7)/(12) .`

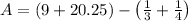
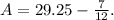
Common denominator:

`A=(351)/(12)-(7)/(12)`

`A=(344)/(12) .`

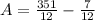
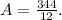
Now, simplify the fraction:

`A=(86)/(3) \approx 28.67`

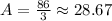
Question:

Using only the definition of Riemann sum and your knowledge of limits, compute the exact area under the curve
`x^2+x^3` between x=1 and x=3.