Final answer:
The function
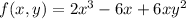 has a local maximum value(s) at (0, 1) and (0, -1), local minimum value(s) at (0, 0), and saddle point(s) DNE.
has a local maximum value(s) at (0, 1) and (0, -1), local minimum value(s) at (0, 0), and saddle point(s) DNE.
Step-by-step explanation:
To find the critical points of the function, we need to calculate the partial derivatives of x and y and set them equal to zero. After finding the critical points, we use the second partial derivative test to determine whether each point is a local maximum, local minimum, or a saddle point.
The partial derivatives are:
![\[ f_x = 6x^2 - 6 + 6y^2 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/84pe2dmsza6v6zn8kuazxkdbmvbinabr4t.png)
![\[ f_y = 12xy \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/pvm1b8gy8y14x7yz1jsc4fivf4625tijqc.png)
Setting
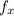 an
an
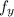 equal to zero, we find that (0, 0) is a critical point.
equal to zero, we find that (0, 0) is a critical point.
Using the second partial derivative test, we evaluate the discriminant
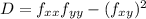 at each critical point. For (0, 0), D > 0, and
at each critical point. For (0, 0), D > 0, and
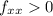 , indicating a local minimum.
, indicating a local minimum.
For the points (0, 1) and (0, -1), D < 0, suggesting saddle points.
Therefore, the function has a local minimum value(s) at (0, 0) and saddle point(s) at (0, 1) and (0, -1).