Question

4 (iii) A tangent is drawn to the graph of y = 5+8x-7x³. The gradient of the tangent is -28. Find the coordinates of the two possible points where this tang​

Answer 1

`\left(-(2√(21))/(7),(35+8√(21))/(7)\right)\;\; \textsf{and}\;\;\left((2√(21))/(7),(35-8√(21))/(7)\right)`

Explanation:

The tangent line of a curve is a straight line that touches the curve at a specific point, sharing the same gradient as the curve at that point.

To find the gradient of the tangent line to a curve at a specific value of x, we need to differentiate the function with respect to x.

The derivative represents the instantaneous rate of change of the function at that point and gives us the gradient of the tangent line at that specific x-value.

Given equation:

`y=5+8x-7x^3`

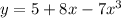
Differentiate the equation:

`\begin{aligned}\frac{\text{d}y}{\text{d}x}&=0+1\cdot 8x^(1-1)-3 \cdot 7x^(3-1)\\\\\frac{\text{d}y}{\text{d}x}&=8-21x^2\end{aligned}`

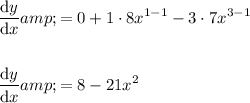
To find the x-coordinates of the two possible points when the gradient of the tangent line is -28, set the derivative to -28 and solve for x:

`\begin{aligned}\frac{\text{d}y}{\text{d}x}&=-28\\\\\implies 8-21x^2&=-28\\\\-21x^2&=-36\\\\x^2&=(-36)/(-21)\\\\x^2&=(12)/(7)\\\\x&=\pm \sqrt{(12)/(7)}\\\\x&=\pm (√(12))/(√(7))\\\\x&=\pm (√(12)\cdot √(7))/(√(7)\cdot √(7))\\\\x&=\pm (√(84))/(7)\\\\x&=\pm (2√(21))/(7)\end{aligned}`

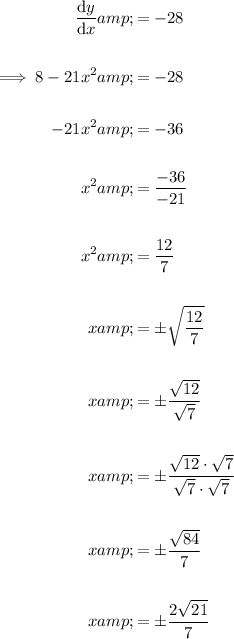
To find the corresponding y-coordinates of the points, substitute each x-coordinate into the original equation:

`\begin{aligned} x=-(2√(21))/(7) \implies y &= 5+8\left(-(2√(21))/(7)\right)-7\left(-(2√(21))/(7)\right)^3\\\\y &= 5-(16√(21))/(7)+(24√(21))/(7)\\\\y &= 5+(8√(21))/(7)\\\\y&=(35+8√(21))/(7)\end{aligned}`

`\begin{aligned} x=(2√(21))/(7) \implies y &= 5+8\left((2√(21))/(7)\right)-7\left((2√(21))/(7)\right)^3\\\\y &= 5+(16√(21))/(7)-(24√(21))/(7)\\\\y &= 5-(8√(21))/(7)\\\\y&=(35-8√(21))/(7)\end{aligned}`

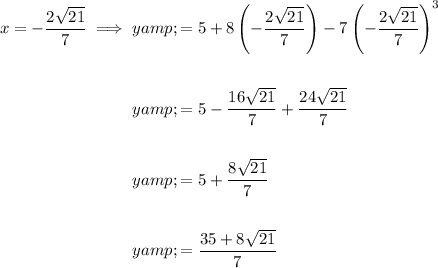
Therefore, the exact coordinates of the two points where the gradient of the tangent line is -28 are:

`\left(-(2√(21))/(7),(35+8√(21))/(7)\right)\;\; \textsf{and}\;\;\left((2√(21))/(7),(35-8√(21))/(7)\right)`