Question

3. Lauren is 3 times older than Megan. The sum of their ages is 78.

How old is each girl?
(LET X = Megan's Age)

Answer 1

Hello!

Answer:

`\Large \boxed{\sf Megan =19.5 }\\\Large \boxed{\sf Lauren =58.5 }`

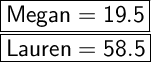
Explanation:

Let be "x" the age of Megan.

So the age of Megan is:

`\sf x`

So the age of Lauren is:

`\sf 3 * x = 3x`

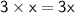
The sum of their ages is 78.

So we have the equation:

`\sf x + 3x = 78`

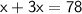
We have just to solve x in this equation to find the age of the girls:

`\sf x + 3x = 78`

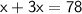
◼ Simplify the side:

`\sf4x = 78`

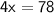
◼ Divide both sides by 4:

`\sf (4x)/(4) = (78)/(4)`

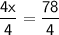
◼ Simplify the fraction:

`\sf x = 19.5`

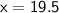
The age of Lauren is 3 times the age of Megan.

The age of Lauren is:

`\sf 19.5 * 3 = 58.5`

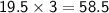
Let's check that the sum of their ages is indeed 78:

`\sf 19.5 + 58.5 = 78`

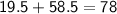
So the age of Megan is 19 and a half years old.

So the age of Lauren is 58 and a half years old.

Answer 2

Megan is 19.5 and Lauren is 58.5 (years old).

Explanation:

Let L be Lauren's age.

We are told that Lauren (L) is three times older than Megan (M), so we can write:

L = 3X

We also learn that the sum of L + X is 78:

L + X =78

Use L=3x in the above equation:

3X + X = 78

4X = 78

X = 19.5

From L=3X:

L = 3*(19.5)

L = 58.5

Lauren is 19.5 and Megan is 58.5.

CHECK:

Is Megan 3 times older than Lauren?

(58.5/19.5) = 3 YES

Is the sum of their ages 78?

19.5 + 58.5 = 78 YES