Question

Find the height of the tree below. (Round to the nearest whole number).

45°
20 ft
75°

Answer 1

Explanation:

Let's name the triangle and necessary angles first so you may understand properly (refer to the attachment).

Now you can see in the picture that angles z and 75° lie in a straight line. The angle of a straight line is 180° means that angle z and 75° should add up to 180.

∠z + 75° = 180°

∠z= 180° - 75°= 105°

So we got angle z now to find the height of the tree we need at least one known side for the triangle ACD.

We can do that by sine law, To use sine law we need the angle opposite the known side which is angle w. We know that the sum of angles in a triangle adds up to 180°, W can find the angle w by constructing an equation.

∠w + ∠z + 45°= 180°

∠w + 105° + 45°=180°

∠w= 180° - (105° + 45°)

∠w= 30°

Now we can use the Sine rule. The sine rule is Sine of an angle divided by its opposite is equal to the sine of another angle divided by its opposite. Even the reciprocal is correct.

`(Sin 45)/(E)` =
`(Sin 30)/(20)`

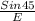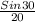
E Sin30° = 20Sin 45° (cross multiplication)

E=
`(20Sin 45)/(Sin 30)`

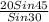
E= 28.28427125 = 28 ft

Now look at the picture. You will notice that the tree is perpendicular to CD which means that its base has an angle of 90°

Remember the trigonometry concept.

Some People Have Curly Brown Hair Through Proper Brushing.

Which represents Sin∅ = p/h, Cos∅ = b/h, Tan∅= p/b.

The letters stand for:

h- hypotenuse which is the side opposite to the right angle.

b- The side which has two angles.

p- The other side which is between the hypotenuse and base here unknown.

I will label everything in the triangle for you to understand.

So we have E which is the hypotenuse and we need to find the perpendicular DA.

Sin 75°=
`(p)/(28)`

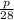
p (DA)= 28Sin 75°

DA= 27.04592314= 27 ft