Question

Use the values In 4 1.3 and In 50≈ 3.9 to find the approximate value of log4 50.

answer choices:
O log4 50 5.07
O log4 50 3
O log4 50 5.2
O log4 50≈ 0.333

Answer 1

log₄50 ≈ 3

Explanation:

To find the approximate value of log₄50, we can use the logarithmic identity that relates logarithms with different bases:

`\log_ab = (\log_cb)/(\log_ca)`

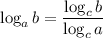
In this case, we can use Euler's number, e, as the common base.

`\log_450 = (\log_e50)/(\log_e4)`

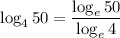
As log with base e is the natural logarithm (ln), we can rewrite it as:

`\log_450 = (\ln50)/(\ln4)`

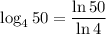
Given that ln 4 ≈ 1.3 and ln 50 ≈ 3.9, we can substitute these values into the formula:

`\log_450 \approx (3.9)/(1.3)`

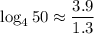
Simplifying the expression:

`\log_450 \approx 3`

Therefore, the approximate value of log₄50 is 3.