Question

Use Newton's method to find all solutions of the equation correct to six decimal places. (Enter your answers as a comma-separated list.)

6 cos(x) = x + 1

Answer 1

1.196076, -1.685255, -4.158089

Explanation:

To find the solutions of the equation 6 cos(x) = x + 1 using Newton's method, we need to perform iterations to converge to the roots.

`\boxed{\begin{array}{c}\underline{\sf Newton-Rhapson\;iteration\;formula}\\\\x_(n+1)=x_n-(f(x_n))/(f'(x_n))\\\\\end{array}}`

If 6 cos(x) = x + 1 then:

`f(x) = 6\cos(x)-x-1`

`f'(x)=-6 \sin(x)-1`

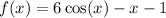
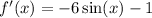
Putting this into the Newton-Raphson formula gives:

`x_(n+1)=x_n-(6\cos(x_n)-(x_n)-1)/(-6 \sin(x_n)-1)`

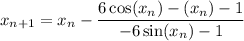
Starting with x₀ = 1, this gives:

`x_(1)=1-(6\cos(1)-1-1)/(-6 \sin(1)-1)=1.205298\; \sf (6\;d.p.)`

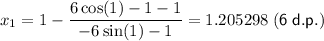
Further iterations give:

`x_2=1.196090\; \sf (6\;d.p.)`

`x_3=1.196076\; \sf (6\;d.p.)`

`x_4=1.196076\; \sf (6\;d.p.)`

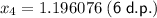
Therefore, one solution is x = 1.196076 (6 d.p.).

Let x₀ = -2:

`x_(1)=-2-(6\cos(-2)-(-2)-1)/(-6 \sin(-2)-1)=-1.664059\; \sf (6\;d.p.)`

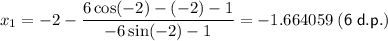
Further iterations give:

`x_2=-1.685228\; \sf (6\;d.p.)`

`x_3=-1.685255\; \sf (6\;d.p.)`

`x_4=-1.685255\; \sf (6\;d.p.)`

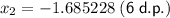
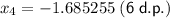
Therefore, another solution is x = -1.685255 (6 d.p.).

Let x₀ = -4:

`x_(1)=-4-(6\cos(-4)-(-4)-1)/(-6 \sin(-4)-1)=-4.166377\; \sf (6\;d.p.)`

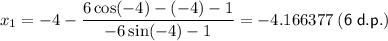
Further iterations give:

`x_2=-4.158107\; \sf (6\;d.p.)`

`x_3=-4.158089\; \sf (6\;d.p.)`

`x_4=-4.158089\; \sf (6\;d.p.)`

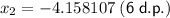
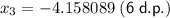
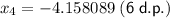
Therefore, the third solution is x = -4.158089 (6 d.p.).

Therefore, the solutions to the equation 6 cos(x) = x + 1 correct to six decimal places are:

• x = 1.196076
• x = -1.685255
• x = -4.158089