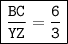Question

O YZ/BC = 6/3
O B= O BC/YZ= 6/3
O

Answer 1

`\boxed{\tt ( BC )/(YZ)=(6)/(3)}`

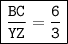
Explanation:

Given:

`\tt (AB)/(XY) =(4)/(2)`

`\tt (AC)/(XZ) =(√(52))/(√(13))=(2)/(1)`

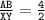
what is left
ΔABC
`\sim` Δ XYZ by SSS similarity theorem.

To be a similar triangle the ratio of the corresponding side should be

The ratio of corresponding side lengths in ΔABC ~ ΔXYZ is:

`(AB)/(XY) = (AC)/(XZ) = (2)/(1)`

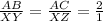
Here one corresponding side's ratio is left.

The one corresponding side
`( BC )/(YZ)=(2)/(1).`

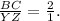
let's see the option,

`( YZ )/(BC)=(6)/(3)=(2)/(1).`

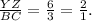
since here,
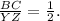`( BC )/(YZ)=(1)/(2).` so, we cannot say this is the correct answer.

let's see the second option:

∡B ≅ ∡Y

since one angle cannot determine a similar triangle,

so, we cannot say this is the correct answer.

Let's see the third option

`( BC )/(YZ)=(6)/(3)=(2)/(1)`

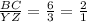
since the corresponding side ratio is
`(2)/(1)`,

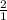so,

so, we can say this is the correct answer.

Therefore,

The answer is option third.

`\boxed{\tt ( BC )/(YZ)=(6)/(3)}`