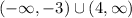Answer:
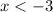 or
or
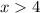
Explanation:
Trickier Method (but more direct)
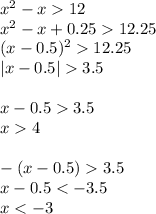
Easier Method (test values required)
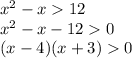
Since
 has the solutions
has the solutions
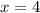 and
and
 , then either all possible solutions to the original inequality are between 4 and -3, or outside of that.
, then either all possible solutions to the original inequality are between 4 and -3, or outside of that.
If we test a value such as
 for example, notice the following:
for example, notice the following:
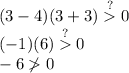
This tells us that all possible solutions are not between 4 and -3, therefore,
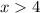 or
or
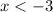 .
.
In interval notation, this would be