Question

11 A table of values for the exponential function f is shown below.

X
1
2
3
4
5
Which situation could describe this function?
f(x)
140,000
143,850
147,806
151,871
156,047
A The value of a house increases by approximately 22% % per year.
K
D The value of a house decreases by $3,850 per year.
घ
B The value of a house increases by $3,850 per year.
C The value of a house decreases by approximately 22% % per year.

Answer 1

A) The value of a house increases by approximately 2 3/4% per year.

Explanation:

The table of values for the exponential function f is:

`\begin{array}c\cline{1-2}\vphantom{\frac12}x&f(x)\\\cline{1-2}\vphantom{\frac12}1&140,000\\\cline{1-2}\vphantom{\frac12}2&143,850\\\cline{1-2}\vphantom{\frac12}3&147,806\\\cline{1-2}\vphantom{\frac12}4&151,871\\\cline{1-2}\vphantom{\frac12}5&156,047\\\cline{1-2}\end{array}`

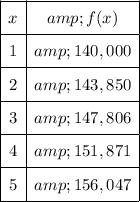
Looking at the given values, we observe that f(x) is increasing as x increases. Therefore, f(x) is an exponential growth function.

The formula for an exponential growth function is:

`f(x)=a(1+r)^x`

where:

• a is the initial value.
• (1 + r) is the base.
• r is the rate of growth (in decimal form).

To find the base of the exponential function, divide each term by its preceding term:

`(156047)/(151871)=1.0275\; \sf (4\;d.p.)`

`(151871)/(147806)=1.0275\; \sf (4\;d.p.)`

`(147806)/(143850)=1.0275\; \sf (4\;d.p.)`

`(143850)/(140000)=1.0275\; \sf (4\;d.p.)`

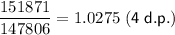
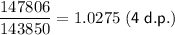
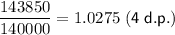
To find the growth rate (r), subtract 1 from the base:

`\begin{aligned}1+r&=1.0275\\1+r-1&=1.0275-1\\r&=0.275\\r&=2.75\%\\r&=2\: (3)/(4)\%\end{aligned}`

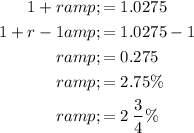
Therefore, situation that could describe function f(x) is:

• A) The value of a house increases by approximately 2 3/4% per year.