Answer:
1. We can find the zeros of the equation using factoring, completing the square, and applying the quadratic formula.
2. We can convert the equation into vertex form
3. We can find the solution to the linear-quadratic system by using a graph.
Explanation:
1.
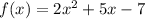 can be factored into
can be factored into
 . To find the zeros, we can set up two equations:
. To find the zeros, we can set up two equations:
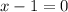 and
and
 . This gives us solutions of
. This gives us solutions of
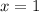 and
and

We can also solve this equation by completing the square.
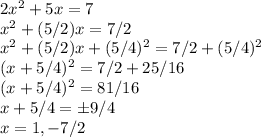
The final way to solve the zeros of the quadratic is by applying the quadratic formula.
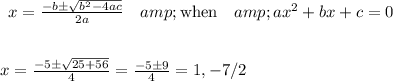
2. To determine the vertex of the equation, we can use the line of symmetry.
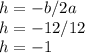
This is our x value.
We can plug x= -1 into the main equation.
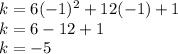
This is our y value.
The vertex is (-1, -5).
3. We can use a graph to find the solution(s) to the two equations.
Thus, the two solutions are (0.354, 1.708) and (5.646, 12.292).