Question

Evaluate the indefinite integral by using the substitution u=x^2+18.

Answer 1

=1 / (x²+18)^6 -6 + c

Explanation:

let u = x² + 18

by applying derivative on both sides,

du = (x² + 18) dx

derivative of a constant i.e. 18 is always 0

derivative of x² = n.x^n-1 = 2.x^2-1 = 2x

thus,

du = 2x * dx

du/2x = dx

thus,

∫ 2x * u^-7 * dx

=∫ 2x * u^-7 * du/2x

=∫u^-7 * du

∫u.du = u^n+1/n+1 + c

thus,

∫u^-7.du = u^-7+1/-7+1 + c

=u^-6/-6 + c

by substituting value of u,

dx = (x²+18)^-6/-6 + c

= 1 / (x²+18)^6 -6 + c

Answer 2

`\displaystyle \int 2x(x^2+18)^(-7)dx= -(1)/(6(x^2+18)^6) + C`

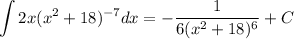
Explanation:

To evaluate the indefinite integral using the u-substitution method.

What is u-substitution?

The basic idea behind u-substitution is to replace a part of the expression in the integral with a new variable, u, in such a way that the integral becomes simpler or more manageable. This new variable is chosen to simplify the integrand or match a known integral form.

`\hrulefill`

Now solving, we have the integral:

`\displaystyle \int 2x(x^2+18)^(-7)dx`

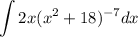
The problem gave us the substitution, u = x² + 18. Now, we need to find the derivative of u with respect to x and solve for dx in terms of du:

`\text{We have,} \ u=x^2+18\\\\\\\Longrightarrow (du)/(dx) = 2x\\\\\\\therefore dx=(du)/(2x)`

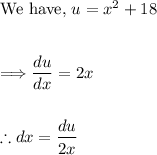
Substituting u and dx in terms of du into the integral expression, we have:

`\displaystyle \int 2x(x^2+18)^(-7)dx \ \longrightarrow \displaystyle \int 2x(u)^(-7) (du)/(2x)`

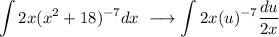
The x terms in the numerator and denominator cancel out, leaving us with:

`\Longrightarrow \displaystyle \int (u)^(-7)du`

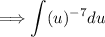
Now, we can integrate with respect to u:

`\Longrightarrow \displaystyle \int (u)^(-7)du\\\\\\\\\Longrightarrow -(1)/(6) \cdot (u)^(-6)\\\\\\\\\Longrightarrow -(1)/(6u^6)`

Plugging our value of u back in we get:

`\Longrightarrow -(1)/(6(x^2+18)^6) + C`

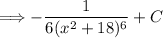
Thus, the indefinite integral using the u-substitution method is solved.