Answer:
The gravitational acceleration in this orbit would be
 the value on the surface.
the value on the surface.
Step-by-step explanation:
This question can be solved by analyzing the equation for the gravitational field strength outside a sphere.
Assume that the mass of Mars is symmetrically distributed with respect to its center, such that the center of mass of the planet would be at its geometric center.
At a distance of
 from the center of mass of a sphere (outside the sphere,) the gravitational field strength, or equivalently the acceleration of gravity, would be:
from the center of mass of a sphere (outside the sphere,) the gravitational field strength, or equivalently the acceleration of gravity, would be:
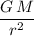 ,
,
Where:
 is the gravitational constant, and
is the gravitational constant, and
 is the mass of the sphere (mass of Mars.)
is the mass of the sphere (mass of Mars.)
Let
 denote the radius of Mars. Under the assumptions, distance from the center of mass of the planet would be
denote the radius of Mars. Under the assumptions, distance from the center of mass of the planet would be
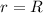 on the surface of the planet. The gravitational field strength would be:
on the surface of the planet. The gravitational field strength would be:
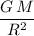 .
.
At a distance of
 from the surface of the planet, the distance from the center of mass of the planet would become
from the surface of the planet, the distance from the center of mass of the planet would become
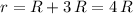 . The gravitational field strength would be:
. The gravitational field strength would be:
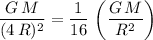 .
.
In other words, the acceleration of gravity in this orbit would be
 the value on the surface.
the value on the surface.