Question

Given coordinate points: (-10,3) (-11,6) Find the slope:

Answer 1

-3

Explanation:

The slope of a line is defined as the change in "y" over the change in "x", or Δy/Δx, and indicates both the direction and steepness of the line. To find the slope given two coordinates, we can use the slope formula. The slope formula is
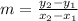`m = (y_(2) - y_(1) )/(x_(2)-x_(1) )`, where m is the slope, (x₁, y₁) represent the first coordinate, and (x₂, y₂) represent the second coordinate.

The first coordinate given to us is (-10,3), so we determine that to be (x₁, y₁). The second coordinate is (-11,6), which we will use as (x₂, y₂).

Now we can plug the appropriate values into the slope formula.

• 
  `m = (y_(2) - y_(1) )/(x_(2)-x_(1) )`
• 
  `m = (6-3)/(-11-(-10))`
• 
  `m = (3)/(-1)`
• m = -3

The slope of the line running through the coordinates (-10,3) and (-11,6) is -3.