Question

Find an equation of a line tangent to the circel x^2 (y-3)^2=34 at the poibnt (5,0)

Answer 1

To find the equation of the tangent line to the circle, differentiate the equation of the circle and substitute the given point. Solve for the derivative to find the slope of the tangent line. Use the point-slope form of a line to write the equation of the tangent line: y = 3x - 15.

Step-by-step explanation:

To find the equation of the tangent line to the circle, we need to find the slope of the circle at the given point (5,0). Using the equation of the circle, we can differentiate both sides with respect to x to find the slope of the tangent line. The derivative of x^2(y-3)^2=34 is 2x(y-3)^2 + x^2(2(y-3))(y-3)' = 0. Substituting the coordinates of the point (5,0) into the derivative equation, we can solve for the slope of the tangent line. Once we have the slope, we can use the point-slope form of a line to find the equation of the tangent line.

The derivative equation is 2x(y-3)^2 + x^2(2(y-3))(y-3)' = 0.

Substituting the coordinates (5,0) into the equation: 2(5)(0-3)^2 + (5)^2(2(0-3))(y-3)' = 0.

Simplifying: 2(5)(-3)^2 + (5)^2(2(0-3))(y-3)' = 0.

Expanding and solving for (y-3)': 2(5)(9) + (5)^2(2(-3))(y-3)' = 0. 90 - 30(y-3)' = 0. -30(y-3)' = -90. (y-3)' = -90/(-30) = 3.

So, the slope of the tangent line is 3. The equation of a line with slope 3 passing through the point (5,0) can be written as y = mx + b, where m is the slope and b is the y-intercept. Substituting the values, we get y = 3x - 15. Therefore, the equation of the tangent line to the circle at the point (5,0) is y = 3x - 15.

Answer 2

The equation of the line tangent to the circle x² + ( y - 3 )² = 34 at the point (5, 0) is
`y = -(3)/(5) x + 3`.

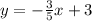Given the parameter:

The equation of the circle is: x² + ( y - 3 )² = 34

Equation of the tangent line at point (5, 0) =?

First, we find the slope of the radius at the point of tangency (5,0):

x² + ( y - 3 )² = 34

Differentiate both sides with respect to x:

2x + 2( y - 3 )(dy/dx) = 0

Now, plug in the coordinates of the point(5,0)

2(5) + 2( 0 - 3 )(dy/dx) = 0

Simplifying, we get:

10 + 2(-3 )(dy/dx) = 0

10 - 6(dy/dx) = 0

6(dy/dx) = 10

dy/dx = 10/6

dy/dx = 5/3

Hence, the slope of the radius at point (5,0) is 5/3

Now, the slope of the tangent line is the negative reciprocal of the slope of the radius.

Hence, slope of the tangent line = -3/5

Plug the slope m = -3/5 and point (5,0) into the point-slope formula and solve for the equation of the tangent line:

y - y₁ = m( x - x₁ )

`y - 0 = -(3)/(5)( x - 5 ) \\\\y = -(3)/(5) x + 3`

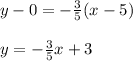
Therefore, the equation of the tangent line is
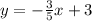`y = -(3)/(5) x + 3`.