Question

Question in picture form

Answer 1

1a) Line 2

1b) Line 1

1c) Line 3

2) Feasible region: Region 2

3) Vertices: (0, 115), (60, 70), (80, 30), (0, 90)

4) $7820, $8480, $7000, $6120

5) 60 standard phones and 70 deluxe phones.

Explanation:

A tech company sells two models of cell phones.

Let x be the number of standard models sold.

Let y be the number of deluxe models sold.

The revenue produced by selling the phones is given by the equation:

`R(x, y) = 62x + 68y`

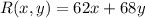
We have been given five constraints represented by the following system of inequalities:

`\begin{cases}3x+4y\leq 460\\3x+4y\geq 360\\2x+y \leq190\\x \geq 0\\ y \geq 0\end{cases}`

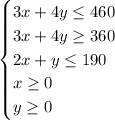
To maximize the revenue produced by selling the phones subject to the given constraints, we need to analyse the feasible region defined by the system of inequalities.

`\hrulefill`

Question 1

The feasible region for the given constraints is the region where all the shaded areas overlap. Therefore, we need to graph the system of inequalities given by the constraints.

Rearrange the first three inequalities so that they are in slope-intercept form:

`\boxed{\begin{aligned}3x+4y& \leq 460\\4y&\leq-3x+460\\y&\leq -(3)/(4)x+115\end{aligned}}`
`\boxed{\begin{aligned}3x+4y& \geq 360\\4y&\geq-3x+360\\y&\geq -(3)/(4)x+90\end{aligned}}`
`\boxed{\begin{aligned}2x+y& \leq 190\\y&\leq-2x+190\\\vphantom{y&\geq -(3)/(4)x+90}\end{aligned}}`

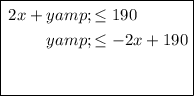
We can determine which lines in the given graph correspond to each constraint by comparing the y-intercepts.

The inequality with the greatest y-intercept is 2x + y ≤ 190.

The inequality with the smallest y-intercept is 3x + 4y ≥ 360.

Therefore:

• a) The line that corresponds to 3x + 4y = 460 is line 2.
• b) The line that corresponds to 3x + 4y = 360 is line 1.
• c) The line that corresponds to 2x + y = 190 is line 3.

`\hrulefill`

Question 2

When graphing an inequality with the sign ≥, draw a solid line and shade above the line.

When graphing an inequality with the sign ≤, draw a solid line and shade below the line.

Graph the inequalities:

• Draw a solid line at y = -(3/4)x + 115 and shade below the line.
• Draw a solid line at y = -(3/4)x + 90 and shade above the line.
• Draw a solid line at y = -2x + 190 and shade below the line.
• For x ≥ 0 shade to the right of the y-axis.
• For y ≥ 0 shade above the x-axis.

The feasible region for the given constraints is the region where all the shaded areas overlap (see attached graph). This is region 2 in the given answer options.

`\hrulefill`

Question 3

The feasible region has four corner points (vertices).

Vertex 1 is the point of intersection between 3x + 4y = 460 and the y-axis. As we have already rearranged the corresponding inequality to slope-intercept form, vertex 1 is (0, 115).

Vertex 2 is the point of intersection between 2x + y = 190 and 3x + 4y = 460. Rearrange the first equation to isolate y, substitute it into the second equation and solve for x. Then substitute the found value of x into the first equation and solve for y:

`\begin{aligned}3x+4(190-2x)&=460\\3x+760-8x&=460\\-5x&=-300\\x&=60\end{aligned}`
`\begin{aligned}2(60)+y&=190\\120+y&=190\\y&=190-120\\y&=70\end{aligned}`

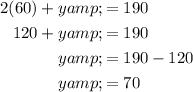
Therefore, vertex 2 is (60, 70).

Vertex 3 is the point of intersection between 2x + y = 190 and 3x + 4y = 360. Rearrange the first equation to isolate y, substitute it into the second equation and solve for x. Then substitute the found value of x into the first equation and solve for y:

`\begin{aligned}3x+4(190-2x)&=360\\3x+760-8x&=360\\-5x&=-400\\x&=80\end{aligned}`
`\begin{aligned}2(80)+y&=190\\160+y&=190\\y&=190-160\\y&=30\end{aligned}`

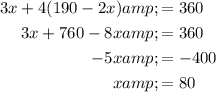
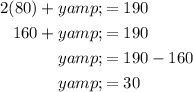
Therefore, vertex 3 is (80, 30).

Vertex 4 is the point of intersection between 3x + 4y = 360 and the y-axis. As we have already rearranged the corresponding inequality to slope-intercept form, vertex 4 is (0, 90).

In summary, the four vertices are:

• (0, 115)
• (60, 70)
• (80, 30)
• (0, 90)

`\hrulefill`

Question 4

Determine the value of R at the vertices by substituting the x and y values of the points into the equation for R:

`\begin{aligned}(0,115) \implies R&=62(0) + 68(115)=\boxed{7820}\\(60, 70) \implies R&=62(60) + 68(70)=\boxed{8480}\\(80, 30) \implies R&=62(80) + 68(30)=\boxed{7000}\\(0, 90) \implies R&=62(0) + 68(90)=\boxed{6120}\end{aligned}`

Therefore, the maximum value of R is 8480 at vertex (60, 70).

`\hrulefill`

Question 5

The maximum weekly revenue is $8,480 at vertex (60, 70).

In the context of this scenario, this means that 60 standard phones and 70 deluxe phones should be produced each week to maximize the weekly revenue.