Question

What is the vertex of g(x)=3x^2-12x+7

Answer 1

`\large\underline{\mathbb{SOLUTION:}}`

Given:

`\bm{g(x)=3x^2-12x+7}`

To find:

`\small\tt{The \: vertex \: of \: the \: parabola.}`

We use the Quadratic Function to solve the vertex:

`\boxed{ \tt{ y =ax {}^(2) + bx + c } }`

`\boxed{\tt{x_(v) = - (b)/(2a)}}`

Let's compare the coefficients to get:

`\longrightarrow \tt{ g(x) = 3 {x }^(2) - 12x + 7}`

`\purple{\tt{a=3, \: b=-12, \: and \: c=7}}`

`\longrightarrow\tt{x_(v) = - (b)/(2a ) = - ( ( - 12))/(2(3)) = (12)/(6) = 2 }`

`\large{\boxed{\purple{\tt{x=2}}}}`

`\therefore` The coordinate of the vertex is
`\rm{x=2}`.

`\qquad \qquad{ \overline{ \qquad \qquad \qquad \qquad \qquad}}`

Substitute in the expression of g(x) to get the corresponding y value as follows:

`\longrightarrow\tt{ g(x) = 3(2 {)}^(2) - 12(2) + 7}`

`\longrightarrow\tt{ = 12 - 24 + 7}`

`\large{\boxed{\purple{\tt{y=-5}}}}`

`\therefore` The coordinate of the vertex is
`\rm{y=-5}`

`\large{\boxed{\rm{The \: vertex \: is \: (2,\: -5)}}}`

`\large\underline{\mathbb{ANSWER:}}`

○
`\tt{(6, \: -5) }`

○
`\tt{(-2, \: -5) }`

◉
`\large{\tt{ \purple{ \large{(2, \: -5)}}}}`

○
`\tt{(-6, \: -5) }`

Answer 2

vertex = (2, - 5 )

Explanation:

given a quadratic function

g(x) = ax² + bx + c ( a ≠ 0 )

then the x- coordinate of the vertex is

`x_(vertex)` = -
`(b)/(2a)`

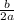
given

g(x) = 3x² - 12x + 7

with a = 3 , b = - 12 , then

`x_(vertex)` = -
`(-12)/(2(3))` = -
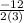`(-12)/(6)` = - (- 2) = 2

to find the y- coordinate , evaluate g(2)

g(2) = 3(2)² - 12(2) + 7 = 3(4) - 24 + 7 = 12 - 17 = - 5

vertex = (2, - 5 )