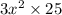The simplified expression without any perfect squares inside the square roots is
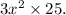
To simplify the expression and remove all perfect squares from inside the square roots, we can apply basic rules of exponents and factorization.
Starting with the given expression:

First, we can break down 10 into its prime factors: 10 = 2 * 5.
Next, we look for perfect squares among the variables' exponents.
 and
and
 are perfect squares since they can be expressed as
are perfect squares since they can be expressed as
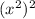 and x^2, respectively.
and x^2, respectively.
Now, we rewrite the expression, factoring out the perfect squares:
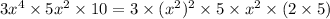
Now, we simplify the expression further:
=
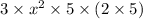
=
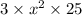
Finally, we rewrite 25 as a perfect square:
 Now we have:
Now we have:
=
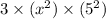
=

=