The magnification of the image is approximately
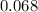 .
.
To solve these problems, we'll consider the spherical Christmas tree ornament as a spherical mirror. Since it's silvered, we'll assume it's a convex mirror (as it's silvered on the inside), which always forms virtual, upright, and reduced images.
Part A: Image Position
For a spherical mirror, the mirror equation is given by:
![\[ (1)/(f) = (1)/(d_o) + (1)/(d_i) \]](https://img.qammunity.org/2024/formulas/physics/high-school/l4mx0hbwqvoq9zbnxbztge1g7edxl72rpg.png)
where:
-
 is the focal length,
is the focal length,
-
 is the object distance (from the mirror's surface),
is the object distance (from the mirror's surface),
-
 is the image distance (from the mirror's surface, with virtual images having a negative value).
is the image distance (from the mirror's surface, with virtual images having a negative value).
For a convex mirror, the focal length is positive and equal to half the radius of curvature, and the radius of curvature
 is half the diameter.
is half the diameter.
Given:
- Diameter of the ornament
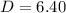 cm,
cm,
- Object distance from the center of the ornament
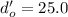 cm.
cm.
To find the object distance from the surface
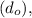 we subtract the radius from the distance from the center:
we subtract the radius from the distance from the center:
![\[ d_o = d_o' - (D)/(2) \]](https://img.qammunity.org/2024/formulas/physics/high-school/jrt0jiwj2x4wo0cqi0x77yemsbcj7c9kg3.png)
The focal length
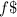 is negative for a convex mirror and is half the radius of curvature
is negative for a convex mirror and is half the radius of curvature
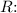
![\[ f = -(R)/(2) = -(D)/(4) \]](https://img.qammunity.org/2024/formulas/physics/high-school/hways66lnlyii750ydz83ydl48ldj5qu84.png)
Then, we solve for
 using the mirror equation.
using the mirror equation.
Part B: Magnification
The magnification
 is given by:
is given by:
![\[ m = -(d_i)/(d_o) \]](https://img.qammunity.org/2024/formulas/physics/high-school/ao24u4zosol98e61yoni38ergjchz9qttl.png)
The negative sign in the magnification formula for spherical mirrors indicates that the image formed by a convex mirror is virtual and upright.
Let's perform these calculations.
Part A: Position of the Image
The position of the image, counting from the ornament surface, is approximately
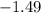 cm. According to the sign convention for mirrors, a negative image distance indicates that the image is virtual and located on the same side of the mirror as the object (i.e., inside the spherical ornament in this case).
cm. According to the sign convention for mirrors, a negative image distance indicates that the image is virtual and located on the same side of the mirror as the object (i.e., inside the spherical ornament in this case).
Part B: Magnification of the Image
The magnification of the image is approximately
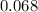 . This value indicates that the image is smaller than the object and upright, as expected for a convex mirror. Since the magnification is less than 1, the image is reduced in size.
. This value indicates that the image is smaller than the object and upright, as expected for a convex mirror. Since the magnification is less than 1, the image is reduced in size.