Question

A dancer is spinning at 72 rpmrpm about an axis through her center with her arms outstretched, as shown in (Figure 1). From biomedical measurements, the typical distribution of mass in a human body is as follows:

Head: 7.0%%
Arms: 13%% (for both)
Trunk and legs: 80.0%%

Suppose the mass of the dancer is 62.0 kgkg, the diameter of her head is 16 cmcm, the width of her body is 24 cmcm, and the length of her arms is 60 cmcm.

A) Calculate moment of inertia about the dancer's spin axis.
Express your answer with the appropriate units.

B) Calculate dancer's rotational kinetic energy.
Express your answer with the appropriate units.

Answer 1

The moment of inertia about the dancer's spin axis is 0.7346 kg
`m^(2)` and her rotational kinetic energy is 20.88 J.

Given:

Mass of the dancer = 62.0 kg

Diameter of her head = 16 cm

Width of her body = 24 cm

Length of her arms = 60 cm

Speed = 72 rpm

The moment of inertia (I) for a rotating object can be calculated using the formula:

`\[ I = \sum m_i r_i^2 \]`

where

`\( m_i \)` = mass of each element of the object

`\( r_i \)` = perpendicular distance of the element to the axis of rotation.

For the dancer's body, three parts are considered to calculate the moment of inertia - the head, the arms, and the trunk/legs.

Head:

`\[ I_{\text{head}} = (1)/(2) m_{\text{(head)}} r_{\text{(head)}}^2 \]`

`\[ m_{\text{(head)}}` = 0.07 x 62

`\[ r_{\text{head}} = (1)/(2) * 16 * 10^(-2) \, \text{m} \]`

`I_((head))=(1)/(2) * 0.07 * 62 * ((1)/(2)*16*10^(-2) )^(2)` = 0.013 kg
`m^(2)`

Arms:

`\[ I_{\text{(arms)}} = 2 * (1)/(3) m_{\text{(arms)}} r_{\text{(arms)}}^2 \]`

`\[ m_{\text{(arms)}}` = 0.13 x 62

`\[ r_{\text{(arms)}} = (1)/(2) * 60 * 10^(-2) \, \text{m} \]`

`I_((head))=2*(1)/(3) * 0.13 * 62 * ((1)/(2)*60*10^(-2) )^(2)` = 0.4836 kg
`m^(2)`

3. Trunk and legs:

`\[ I_{\text{(trunk/legs)}} = (1)/(12) m_{\text{(trunk/legs)}} h_{\text{(trunk/legs)}}^2 \]`

`\[ m_{\text{(trunk/legs)}}` = 0.80 x 62

`\[ h_{\text{(trunk/legs)}} = 24 * 10^(-2) \, \text{m} \]`

`I_((head))=(1)/(12) * 0.80 * 62 * (24*10^(-2) )^(2)` = 0.238 kg
`m^(2)`

Total moment of inertia:

`\[ I_{\text{total}}` = 0.013 + 0.4836 + 0.238 = 0.7346 kg
`m^(2)`

The rotational kinetic energy (KE) can be calculated using the formula:

`\[ KE = (1)/(2) I \omega^2 \]`

where

`\( \omega \)` = angular velocity (rpm).

`\[ \omega = \frac{2\pi * \text{72}}{60} \]` = 7.54 rad/s

KE =
`(1)/(2) * 0.7346 * (7.54)^(2)` = 20.88 J

The moment of inertia and the rotational kinetic energy of the dancer can be calculated as shown above.

Answer 2

A. Moment of inertia is
`\[ I = 1.3135 \, \text{kg} \cdot \text{m}^2 \]`

B .Rotational kinetic energy is approximately 37.335 joules

How to find the moment of inertia and rotational kinetic energy of the dancer?

Moment of Inertia

Given:

Dancer's mass (m) = 55.5 kg

Diameter of the head (d) = 16 cm

Width of the body (w) = 24 cm

Length of the arms (l) = 60 cm

Calculate the radius of gyration for the head (r₁):

`\( r_(1) = (d)/(2) = \frac{16 \, \text{cm}}{2} = 8 \, \text{cm} \)`

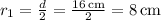
Calculate the radius of gyration for the trunk and legs (r₂):

`\( r_(2) = (w)/(2) = \frac{24 \, \text{cm}}{2} = 12 \, \text{cm} \)`

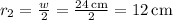
Calculate the radius of gyration for the arms (r₃):

`\( r_(3) = (l)/(2) = \frac{60 \, \text{cm}}{2} = 30 \, \text{cm} \)`

Expression for the moment of inertia for the dancer:

`\[ I = \left((7m)/(100) \cdot r_(1)^2\right) + \left((80m)/(100) \cdot r_(2)^2\right) + \left((13m)/(100) \cdot r_(3)^2\right) \]`

Substitute the given values:

`\[ I = \left(0.07 \cdot 55.5 \, \text{kg} \cdot (8 \, \text{cm})^2\right) + \left(0.80 \cdot 55.5 \, \text{kg} \cdot (12 \, \text{cm})^2\right) + \left(0.13 \cdot 55.5 \, \text{kg} \cdot (30 \, \text{cm})^2\right) \]`

`\[ I = 1.3135 \, \text{kg} \cdot \text{m}^2 \]`

Rotational Kinetic Energy

Expression for rotational kinetic energy:

`\[ K = (1)/(2) \cdot I \cdot \omega^2 \]`

Given:

Angular velocity (ω) =
`\( 72 \, \text{rpm} = 72 * (2\pi)/(60) \, \text{rad/s} \)`

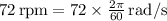
Substitute the values:

`\[ K = (1)/(2) \cdot 1.3135 \, \text{kg} \cdot \text{m}^2 \cdot \left(72 * (2\pi)/(60)\right)^2 \, \text{rad/s} \]`

`\[ K \approx 37.335 \, \text{J} \]`

Therefore, the rotational kinetic energy of the dancer is approximately 37.335 joules.

See missing part of the question on the attached image below,