Question

A 2.0 kg object moving to the right with speed 0.50 m/s A 2.0 kg object moving to the right with speed 0.50 m/s experiences the force shown. What are the object's speed experiences the force shown. What are the object's speed and direction after the force ends? and direction after the force ends? A. 0.50 m/s left A. 0.50 m/s left B. At rest B. At rest C. 0.50 m/s right C. 0.50 m/s right D. 1.0 m/s right D. 1.0 m/s right E. 2.0 m/s right E. 2.0 m/s right Δp

x

=J
x

or p
lix

=p
ix

+J
x

*2015 Pessson Eduxafon, lik. D2015 Persan Edxalici, lik. Slives 9-7

Answer 1

The correct option is b.

The final speed of the object is 0 m/s. Since the speed is 0, the object is at rest. The direction remains to the right as the object was never brought to a stop and was only slowed down.

The object's speed and direction after the force ends can be determined using the impulse-momentum theorem. This theorem states that the net impulse acting on an object is equal to the change in its momentum. In this case, the net impulse is the product of the force and the time it acts for. The change in momentum is the difference between the object's initial momentum and its final momentum.

From the graph, we can see that the force is negative for a time of 0.5 seconds. This means that the force is acting in the opposite direction to the object's motion. Therefore, the net impulse will be negative. The object's initial momentum is 2.0kg⋅0.50m/s=1.0kg⋅m/s.

Step-by-step solution:

1. Identify the relevant quantities:

• Mass of the object: 2.0 kg
• Initial speed of the object: 0.50 m/s (moving to the right)
• Force applied: Negative for 0.5 seconds (acting to the left)

2. Determine the net impulse:

• Impulse is the product of force and time: Impulse = Force × Time
• Since the force is negative, the net impulse is also negative: Net Impulse = -2.0 N × 0.5 s = -1.0 Ns

3. Apply the impulse-momentum theorem:

• The impulse-momentum theorem states: Net Impulse = Change in Momentum
• Expressing momentum as mass multiplied by velocity: Δ(mv) = -1.0 Ns

4. Calculate the change in momentum:

• Initial momentum:
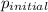  `p_(initial)` = 2.0 kg × 0.50 m/s = 1.0 kg⋅m/s
• Let the final speed be v. Change in momentum: Δp = 2.0 kg × (v - 0.50 m/s)

5. Substitute and solve for the final speed:

• Rewrite the impulse-momentum equation: -1.0 Ns = 2.0 kg × (v - 0.50 m/s)
• Solve for v: v = 0 m/s

Therefore, The answer is 0, so it is in the rest.

The complete question is here:

A
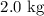`$2.0 \mathrm{~kg}$` object moving to the right with speed
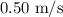`$0.50 \mathrm{~m} / \mathrm{s}$` experiences the force shown. What are the object's speed and direction after the force ends?

A. 0.50 m/s left

B. At rest

C. 0.50 m/s left right

D. 1.0 m/s left right

E. 2.0 m/s left right

Answer 2

The final speed of the object is 1 m/s right (Option D).

How to calculate the final speed of the object?

The final speed of the object is calculated by applying the following formula for Newton's second law of motion as follows;

F = m(v - u)/t

where;

• m is the mass of the object
• u is the initial speed of the object
• v is the final speed of the object
• t is the time of motion of the object

The given parameters include;

the applied force = 2 N

the time of motion, t = 1/2 s = 0.5 s

initial speed, u = 0.5 m/s

mass of the object, m = 2 kg

F = m(v - u)/t

m(v - u) = Ft

v - u = Ft / m

v = (Ft/m) + u

v = (2 x 0.5 / 2) + 0.5

v = 1 m/s

The missing diagram is in the image attached.