Question

In (Figure 1), a=30 mm and b=120 mm. Part A Determine the moment of inertia of the cross-sectional area of the T-beam with respect to the x′ axis passing through the centroid of the cross section. Figure 1 of 1 Express your answer to three significant figures and include the appropriate units.

Answer 1

The moment of inertia (I) of the T-beam's cross-sectional area with respect to the x' axis is
`2.25 × 10^6 mm^4`.

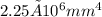Step-by-step explanation:

The moment of inertia (I) for the T-beam's cross-sectional area with respect to the x' axis is determined by employing the formula for a T-beam:
`I = (1/3) * b * h^3 - 2 * [(1/12) * a * (a/2)^3].` Here, a represents the stem's width (30 mm), b symbolizes the flange width (120 mm), and h denotes the total height of the T-beam (120 mm). Plugging in these dimensions, the calculation yields I =
`2.25 × 10^6 mm^4`.

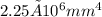This result signifies the distribution of the area around the x' axis, indicating the T-beam's resistance to bending. The formula accounts for the differing contributions of the stem and flange to the overall moment of inertia, reflecting the structural significance of these components in resisting bending moments.

The final numerical value,
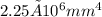`2.25 × 10^6 mm^4`, encapsulates the T-beam's ability to withstand bending forces and is expressed in units of length to the fourth power. Engineers use this property extensively in designing structures to ensure stability and performance under various loading conditions.