Question

PLEASE HELP!!! I DONT UNDERSTAND!

Answer 1

`\textsf{B)} \quad \overline{AC} \cong \overline{BC}`

`\textsf{C)} \quad \overline{AD} \cong \overline{BD}`

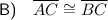
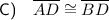
Explanation:

We are told that line CD bisects line segment AB.

In geometry, to bisect means to divide something into two equal parts. So line CD divides line segment AB into two equal parts.

In other words, line CD intersects line segment AB at a point E, so point E is the midpoint of line segment AB. As a result, line segment AE is equal in length to line segment BE:

• 
  `\overline{AE} \cong \overline{BE}`

Although we are not told that line CD is the perpendicular bisector of line segment AB (i.e. CD and AB intersect at right angles), we can deduce this from the construction diagram. Therefore:

• 
  `m \angle AEC = m \angle BEC = 90^(\circ)`

• 
  `m \angle AED = m \angle BED = 90^(\circ)`

The Side-Angle-Side (SAS) Congruence Theorem states that if two sides and the included angle in one triangle are congruent to two sides and the included angle in another triangle, the triangles are congruent.

If we draw line segments AC and BC, we create two congruent triangles ΔAEC and ΔBEC by SAS congruency. The two congruent sides are AE ≅ BE and EC ≅ EC, and the congruent included angles are ∠AEC ≅ ∠BEC. Therefore, AC ≅ BC.

Similarly, if we draw line segments AD and BD, we create two congruent triangles ΔAED and ΔBED by SAS congruency. The two congruent sides are AE ≅ BE and ED ≅ ED, and the congruent included angles are ∠AED ≅ ∠BED. Therefore, AD ≅ BD.

Therefore, the two statements that guarantee that line CD bisects AB are:

• 
  `\overline{AC} \cong \overline{BC}`

• 
  `\overline{AD} \cong \overline{BD}`