Question

Wgat is the solution of the system of equations?

Answer 1

you can just solve for x and plug-in X and solve for Y,

`\begin{bmatrix}y=-2x+8\\ y=x-4\end{bmatrix}`

`x-4=-2x+8`
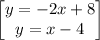
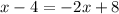
isolate X, solve for X, you get x = 4
you substiute x = 4 to one of the equation, I choose y = x -4
y = 4 - 4 =0
or you can solve via Cramer's rules with a matrix, Which I do not think you need to know

`\begin{bmatrix}y=-2x+8\\ y=x-4\end{bmatrix}\begin{bmatrix}y+2x=8\\ y-x=-4\end{bmatrix}M=\begin{pmatrix}1&2\\ 1&-1\end{pmatrix}`

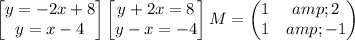
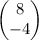`\begin{pmatrix}8\\ -4\end{pmatrix}` will be the answer cloumn

`M_y=\begin{pmatrix}8&2\\ -4&-1\end{pmatrix}`

`M_y=\begin{pmatrix}8&2\\ -4&-1\end{pmatrix}`

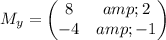
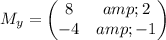
then you get D = -3, Dy = 0, Dx = -12
Thus you get y = 0, x = 4

Answer 2

To solve this system of equations, we can set the expressions equal to each other:

x - 4 = -2x + 8

Now, we can subtract x from both sides:

(x - x) - 4 = (-2x - x) + 8
-4 = -3x + 8

Next, we subtract 8 from both sides:

-4 - 8 = -3x + 8 - 8
-12 = -3x

Finally, we divide by the coefficient:

-12 / -3 = -3x / -3
4 = x

With x, we can plug our result into one of the equations to find y:

y = x - 4
y = 4 - 4
y = 0

Hence, the solution to the system of equations is (4,0). This is best represented by option C.